こんにちは、育伸開発です。
中2理科・電気についての授業2回目になります。前回の授業『【中2理科 電気】回路図の電圧・電流・抵抗値を出せるようにする授業(1)基本編』でオームの法則を使わず回路図の中で電圧・電流・抵抗の値を出すやり方を扱いました。今回はそのつづきの内容となります。
目次
各数値を出すときのポイント
今回学習する上でのポイントは以下の通りです。今はまだざっと読んでおく程度で構いません。
- オームの法則とは、電熱線や抵抗を流れる電流が加えられる電圧に比例するという原則のことである
- 電流・電圧・抵抗のうち2つわかっているところでオームの法則にあてはめて残りの1つを出す
- この時の電流の単位はA(アンペア)のみで使われる
- 全体抵抗は電源の部分の電圧と電流の値からオームの法則に当てはめて出しても良い
- 実際に回路図で数値を出すためにオームの法則を使うとき、以下の図の2か所に数値をあてはめて残りを出す(縦並びの時は分子÷分母の割り算を、横並びの時は掛け算を使って出す)
オームの法則とは
先生:では授業を始めます。気を付け、礼。お願いします!
生徒:お願いします!
先生:今日は続きの内容で、オームの法則を使って回路図の中で数値を出せるようにしていくよ。授業の最後に問題演習をするけど、複合回路で電流・電圧・(全体)抵抗の値を出せるようになるのが目標だ。そこで必要なのがオームの法則についての知識と正しく使えるようになることなので、まずそれを説明しよう。
先生:オームの法則というのは、電熱線や抵抗を流れる電流が加えられる電圧に比例するという原則のことだよ。では質問。20Ωの抵抗に60Vの電圧をかけたら3A の電流が流れたとしよう。そして次に2倍の120Vの電圧をかけたとするなら、何Aの電流が流れるかな?
生徒:6A
先生:ナイス、正解!比例関係が成り立っているので、電流も3A×2=6Aとなるんだ。逆に言うと120V÷20Ω=6Aと電流の値を出すことが出来るよ。こうしていくと電流・電圧・抵抗の関係を3つの式にすることができるんだ。それは以下の通り。
- 電圧(V)=抵抗(Ω)×電流(A)
- 抵抗(Ω)=電圧(V)÷電流(A)
- 電流(A)=電圧(V)÷抵抗(Ω)
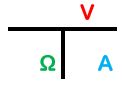
先生:このようになるんだけど、電流・電圧・抵抗のうち2つがわかっているとオームの法則にあてはめて残りの1つを計算で出せるということだよ。ただ、これを丸々覚えるのは大変なので形を変えたものを紹介しよう。実際に使いやすい形にしたのが以下のものだから、それを覚えて。

先生:反時計周りに上から単位がV→Ω→Aとなることを覚えておこう。先生は「ブイオームア」と心の中でブツブツ言ってるよ。慣れてきたら頭の中にこの画像を思い出してすぐ計算出来るようになるけどね。
電流の求め方
先生:例えば10Ωの抵抗があるところに30Vの電圧をかけたら電流は何A流れるのか知りたいとしよう。そのとき、30Vと10Ωという数値を下のオームの法則を表す図に入れるんだ。そうすると以下のようになる。
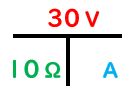
先生:これは2つの数字が上と下に並んでいるので分数になっていると考えよう。分数は割り算の式に直すことができて、分子÷分母になるというルールだ。だから30÷10=3の計算をするということだよ。そして電流の単位であるA(アンペア)をつけて、3Aと出てくるんだ。
抵抗の求め方
先生:同じように抵抗を出したい時は電圧と電流の数値を図に入れよう。100V電圧をかけたら2A電流が流れた場合の抵抗は何Ωか知りたいとすると…
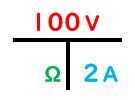
先生:このようになるよ。これって計算式は何になる?
生徒:100÷2
先生:そのとおり。だから100÷2=50Ωと抵抗値が出てくるよ。電流や抵抗の値を求めたい時は電圧(V)を抵抗や電流で割ればいいと意識しておこう。
電圧の求め方
先生:ただし、電圧自身を求める時だけは掛け算の式になるよ。具体的に、30Ωの抵抗に0.5A電流が流れていたら電圧が何Vかかっているのか知りたいとしよう。その時は…
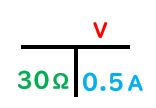
先生:このようになって30と0.5が横並びになったね。横並びの時だけ掛け算の式になるから30×0.5とするんだ。そうすると何Vとなる?
生徒:15V
先生:正解!これが回路図で数値計算するときのオームの法則の使い方だ。ちなみに電流は全部A(アンペア)の単位で行うので、問題文の単位がmA(ミリアンペア)になっていたらA(アンペア)に変換してから計算を始めるようにね。計算結果の単位も A(アンペア)で出てくるから、mA で求めたいときは A から単位変換をしよう。
練習問題
先生:では練習するために3つ問題を出そう。以下計算して解いてみて。小数の入った計算の時はミスしないよう注意しながらやってね。でははじめ!
1.電流が3A、電圧が15Vかかっているところの抵抗は何Ωですか。
2.15Ωの抵抗に電流が400mA流れているときにかかっている電圧は何Vですか。
3.20Ωの抵抗に電圧を4Vかけたら電流は何mA流れますか。
・
・
・
1.電流が3A、電圧が15Vかかっているところの抵抗は何Ωですか。
先生:では答えを確認しよう。1番は何Ωになった?
生徒:5Ω
先生:正解!15÷3=5Ωだ。電圧が出ている時は電圧を別の数字で割ろう。
2.15Ωの抵抗に電流が400mA流れているときにかかっている電圧は何Vですか。
先生:では2番、何Vになった?
生徒:6V
先生:いいね、正解!電圧自身を出す時は掛け算になる。あと400mAを0.4Aと直してから計算だ。15×0.4=6Vとしよう。
3.20Ωの抵抗に電圧を4Vかけたら電流は何mA流れますか。
先生:では3番、何mAになった?
生徒:200mA
先生:素晴らしい、正解!!電圧が出ているので電圧を別の数字で割ろう。4÷20=0.2Aとなる。あくまで電流はA(アンペア)の単位で出てくるから、最後に0.2A=200mAと変換するのを忘れないように。
直列回路のパターン
先生:次に実際の回路図でオームの法則を使いつつ解く問題の例を出すよ。まずは直列回路からやろう。以下の図を見てまず右上の抵抗が何Ωなのか、次に回路全体の抵抗値を出すことを一緒にやろう。
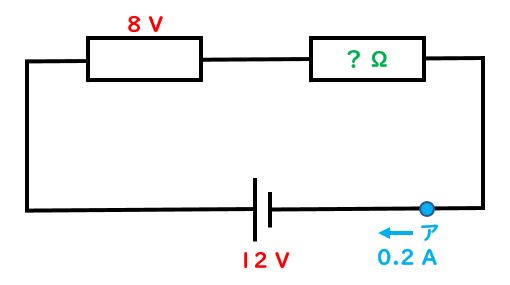
先生:まず右上の「?Ω」の部分を一緒に出していこう。そうするとまず確認するけど、右上の抵抗部分で流れている電流は何A?
生徒:0.2A
先生:正解。直列部分で流れる電流の量はどこも同じだからね。では右上の抵抗部分の電圧は何V?
生徒:4V
先生:正解。電源の電圧12Vのうち8Vを左上の部分で使っているから残りの4Vが右上の抵抗部分で使う電圧だ。ということで、抵抗値以外の数値が電流が0.2A、電圧が4Vとわかったね。そうしたらオームの法則の図に代入して計算だ。計算してみて。何Ωになった?
生徒:20Ω
先生:正解!4V÷0.2A=20Ωとなる。そうすると以下の状態になるのだけど、次にこの回路の全体抵抗が何Ωになるか考えよう。
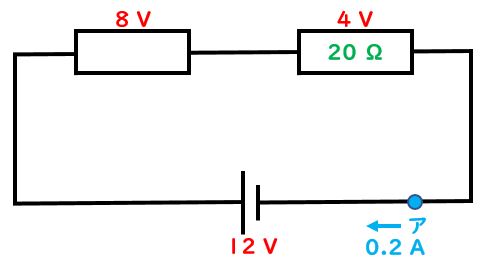
先生:全体抵抗を出す時のやり方だけど2つあるよ。まず1つめ、それぞれの抵抗値を足して出すやり方で解いていこう。この時電流・電圧・抵抗のうち2つわかっているところでオームの法則にあてはめて残りの1つを出すことを心がけよう。そうすると左上の8V電圧がかかっている部分の抵抗値が出るね。何Ωになる?
生徒:40Ω
先生:いいね、正解。8V÷0.2A=40Ωだ。ということは40Ωと20Ωの抵抗が直列に繋がっていることがわかり、その場合の全体抵抗を出せる状態になった。全体抵抗は何Ωになる?
生徒:60Ω
先生:ナイス、正解。直列に繋がっている部分の全体抵抗はそれぞれの抵抗値を足せば出てくるんだったね。ではもう1つのやり方を紹介しよう。全体抵抗を求める時、電源の部分の電圧と電流の値をオームの法則に当てはめて出しても良いよ。最初の図に戻しておこう。

先生:これで電源の部分の電圧と電流を確認していくんだ。何Vと何Aになっている?
生徒:12V、0.2A
先生:そうだね。だからそれをオームの法則にあてはめよう。それで全体抵抗が出るよ。何Ωになる?
生徒:60Ω
先生:正解。12÷0.2=60Ωだ。このように全体抵抗を出す方法は2つあるから、両方使えるようにしておこう。実際に試験なんかで解くときは問題に応じてやりやすい方を使ってね。
並列回路のパターン
先生:次に並列回路を扱うよ。ここでは2つ問題を出すから、それを解くことで理解を深めよう。まず1問目、以下の図でイの部分を流れる電流は何A?
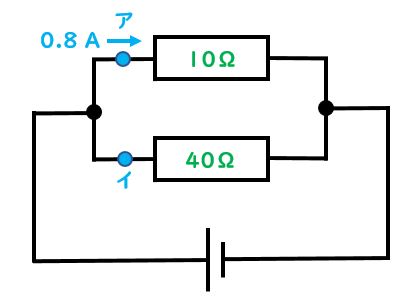
先生:ここでイの部分に注目すると、電流と電圧がわかっていないね。抵抗が40Ωだけど、3つのうち1つだけしかわかっていない時は、残りの2つを出すことは出来ないんだ。そしてふと上を見ると、0.8Aの電流が10Ωの抵抗の部分を流れていることがわかる。だからその部分でオームの法則にあてはめて残りの1つを出してみよう。
先生:そうすると上の部分にかかっている電圧は何V?
生徒:8V
先生:いいね、正解。10×0.8=8Vだ。その瞬間、並列部分の電圧がどのようにかかるかを考えて、40Ωの部分にかかる電圧がわかるようになったね。何V?
生徒:8V
先生:そのとおり、正解!並列部分では電圧は同じ力がかかるんだった。そしてわかったことを書き加えると以下の図のようになる。40Ωの部分でオームの法則に当てはめることが出来るようになったね。
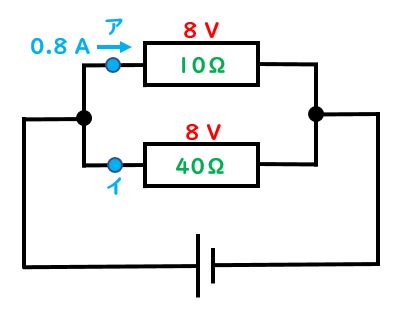
先生:ではイの部分を流れているのは何A?
生徒:0.2A
先生:正解!8÷40=0.2Aだね。1問目の答えだ。では2問目、以下の図でこの回路の全体抵抗は何Ω?
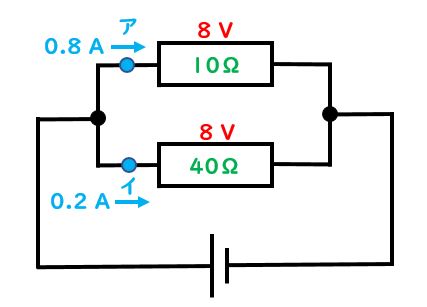
先生:全体抵抗の求め方は2パターンあったね。1つ目のやり方だけど、逆数を足して逆数にして出すというものだった。このやり方で出してみよう。復習練習ということで、計算してみて。でははじめ!
・
・
・
先生:では確認するよ。何Ωになった?
生徒:8Ω
先生:ナイス、正解!10と40という数字の逆数は1/10と1/40だね。そうすると以下のように逆数を足していってその結果を逆数にすると…
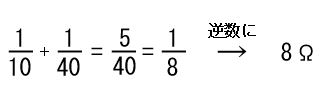
先生:8Ωと出てくる。これが答えだ。2つ目の全体抵抗の出し方も確認しておこう。それは電源の部分の電圧と電流の値をオームの法則に当てはめて出すというものだった。
 先生:では聞くけど、上の図で電源の電圧は何Vで、電流は何Aだと言える?
先生:では聞くけど、上の図で電源の電圧は何Vで、電流は何Aだと言える?
生徒:8V、1A
先生:いいね。並列回路では8Vの電圧を1回一気に使っておしまいだから電源も8V、電流は0.8Aと0.2Aの量を合流させている部分だから足して1Aになる。そうしたら8Vと1Aをオームの法則の図に当てはめよう。全体抵抗は何Ωになる?
生徒:8Ω
先生:ナイス、正解!8÷1=8Ωだ。
総合練習問題(複合回路)
先生:ここまでの学習でオームの法則にあてはめていろいろな数値を出すやり方がわかったところだと思う。そうしたら最後に複合回路を2つ出すから、それについての問題演習を行おう。以下ダウンロードプリントを用意しているので、それを解いて。解き終わったら答え合わせと解説を行うので戻ってきてね。でははじめ!
回路図とオームの法則 問題 (201 ダウンロード) 回路図とオームの法則 解答 (166 ダウンロード)
先生:以下画面見ながら解けるよう問題を載せておこう。
図1・図2の回路図について、以下の問いに答えなさい。
図1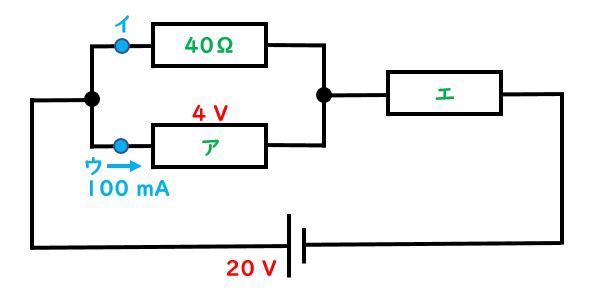
(1)アの抵抗は何Ωですか。
(2)イを流れる電流は何mAですか。
(3)エの抵抗は何Ωですか。
(4)回路全体の抵抗は何Ωですか。
図2
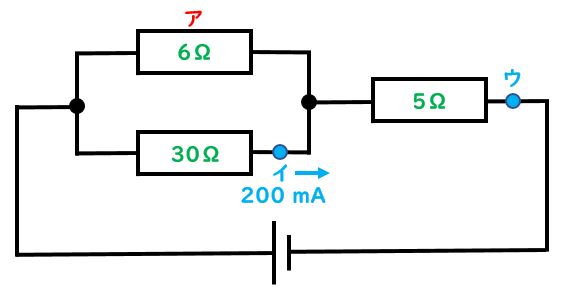
(5)アにかかっている電圧は何Vですか。
(6)ウを流れる電流は何mAですか。
(7)回路全体の抵抗は何Ωですか。
総合練習問題の解答
先生:では答え合わせをしよう。以下の解答を確認してね。
図1について
(1)40Ω
(2)100mA
(3)80Ω
(4)100Ω
図2について
(5)6V
(6)1200mA
(7)10Ω
総合練習問題の解説
先生:解説を入れよう。必要な部分だけ確認してね。
解説(1)
オームの法則を使う時の電流の単位は常にアンペア(A)だった。だから100mA=0.1Aと変換してオームの法則を使おう。4V÷0.1A=40Ωだ。
解説(2)
並列部分の電圧は同じになるので40Ωの部分も4Vの電圧がかかっている。そこで4Vと40Ωをオームの法則にあてはめて、4V÷40Ω=0.1Aと出そう。何mAですかと聞かれているので、アンペア(A)をミリアンペア(mA)に単位変換するのを忘れずに。0.1A=100mAだ。
解説(3)
並列部分で電圧が4Vかかっているので、以下の図の状態になると考えよう。4Vとエの部分の電圧を足すと電源の20Vとなることからエの電圧が16Vだとわかる。
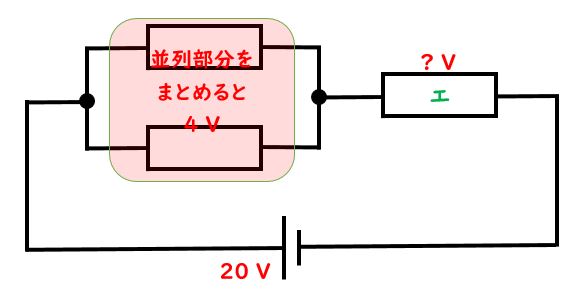
また、イとウの電流を足した0.2Aの電流がエの部分で流れているとわかる。そうしたら16Vと0.2Aをオームの法則に当てはめて抵抗値を出そう。16V÷0.2A=80Ωだ。
解説(4)
電源の電圧が20V、電流が0.2Aとわかっている。そのため今回は全体の電圧、電流がそれぞれ20V、0.2Aであると考え、それをオームの法則に当てはめよう。20V÷0.2A=100Ωだ。別解として並列部分の抵抗を計算して20Ωと出し、それにエの抵抗値80Ωを足して100Ωと出しても良いよ。
解説(5)
まず30Ωの部分に200mA(=0.2A)の電流が流れていることに着目しよう。この2つをオームの法則に当てはめて30Ω×0.2A=6Vと電圧が出る。並列部分では同じ電圧がかかるのでアの部分も6Vだ。
解説(6)
6Ωのところに6Vの電圧がかかっていることが(5)の問題でわかったところだ。6Ωと6Vをオームの法則に当てはめて、6V÷6Ω=1Aとなる。その1Aとイの0.2Aの電流が合わさってウの部分へ流れるので1.2Aだとわかる。何mAなのかを聞かれているので単位を変換して1.2A=1200mAとなる。
解説(7)
まず計算で並列部分の抵抗を出そう。1/6+1/30=1/5となる。それを逆数にするので5Ωとわかる。そうしたら回路全体の抵抗は並列部分の5Ωと直列に繋がっている右上の5Ωを足して10Ωとなる。
別解として、並列部分の6Vと右上の抵抗部分でかかっている電圧6V(5×1.2=6V)を足して電源部分の電圧を12Vと出す→ウを流れる電流が1.2Aであることから電源部分も1.2Aとわかる→12Vと1.2Aをオームの法則に当てはめて12V÷1.2A=10Ωと出しても良いよ。
先生:出来具合はどうだったかな?間違えたところは明日と1週間後の2回は解き直して正しい解き方を定着させておこう。では今日の授業はおしまいです。気を付け、礼。ありがとうございました^^
2回に分けて行った電気分野の授業はこれで終了です。質問がある方はコメント欄を使って下さい。ではまた!