【中2数学 1次関数】動点とグラフのわかりやすい授業

こんにちは、育伸開発です。

今回は中2で学習する1次関数の応用・動点の問題の授業を行います。この問題は多くの生徒が苦手とするものです。点が動いていくのを把握するのが難しく、場所によって変域が変わってきます。それぞれの変域で関数の式も変わってくるので難しいと感じるのは無理もありません。

そんな生徒に向けての授業を用意しました。決まったパターンがありますから、それを押さえて手順どおりに作業を進めていきましょう。何問か解いて慣れれば解く力が付き、解けるようになります。

中3の2次方程式の単元でも動点の問題が出てきますから、中2のうちに慣れておくと後で楽になります。

復習できるようダウンロードできるプリントも用意しました。定期テストに向けて頑張るみなさんを応援します。頑張って下さい！

動点の文章問題を解く時の手順

動点の問題を解くには手順が4つあります。まずはサラッと確認しておいて下さい。具体的には問題を解いていくことで何を意味しているのかわかるようになります。

1. ｘの変域を分けて表す
2. 必要な部分の長さを文字式で表す
3. 文字式で面積を表す
4. 変域から座標を出してグラフにする

では模擬授業を始めます。

問題１：動点の移動距離を使う問題Ⅰ

先生：では授業をはじめます。気をつけ、礼。お願いします！今日は数学の1次関数の応用問題を扱っていくよ。動点の問題だ。

生徒：それって点が動くやつですか。

先生：そう。この問題は苦手とする人が多いよ。でも大丈夫。じっくり解説しながら授業を進めていくから一つ一つやっていけば解けるよ。そうしたらあとは慣れていくだけだ。まず手順を４つ紹介しよう。

1. ｘの変域を分けて表す
2. 必要な部分の長さを文字式で表す
3. 文字式で面積を表す
4. 変域から座標を出してグラフにする

先生：この通りにやっていけば答えを出せるようになるよ。では早速問題を1つ出すから、一緒に解いて行こう。

1－1：変域を分けて表す

先生：ＢＰ＝ｘと文字式で表すことが出来るよ。そうすると点Ｐが（1）辺ＢＡ上にある時、ｘの変域はどうなる？

生徒：0≦ｘ≦4

先生：ナイス、その通り。点Ｐが4㎝移動すると点Ａに到着して、そこから先は辺ＡＤ上を移動するからね。では点Ｐが（2）辺ＡＤ上にあるときの変域はどうなる？

生徒：4≦ｘ≦8

先生：いいね、正解。ＢからＡを通ってＤまで点Ｐが進むのだけど、4㎝移動したＡが辺ＡＤ上の最初の場所だ。そして…

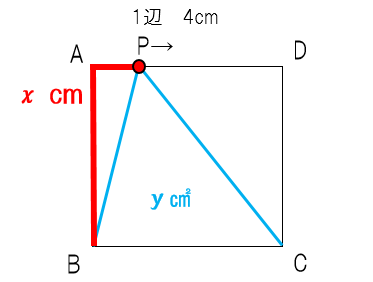
先生：図のようにｘが8㎝移動するとＤに到着するね。ということでｘの変域は 4≦ｘ≦8 だ。では点Ｐが（3）辺ＤC上にあるときの変域はどうなる？

生徒：8≦ｘ≦12

先生：ナイス！ＤからＣまでの長さが4㎝だから…

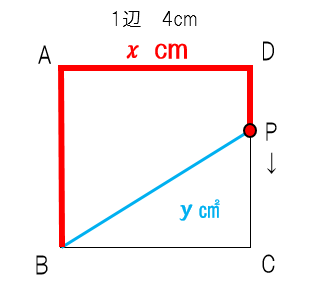
先生：8㎝移動したところから始まって、12㎝移動するとCに到着するね。ということでｘの変域は 8≦ｘ≦12 だ。ここまでで手順1が終わったよ。まとめると以下の通りだ。

1－2：変域ごとに文字式で面積を表す

先生：そうしたら次に手順2として、必要な部分を式で表そう。そして手順3として、 y= の形で三角形の面積を文字式で表すよ。まずは（1）だけどＰＢが△ＰＢＣの高さになっているね。そうすると底辺にあたるＢＣの長さを知りたいんだ。そのＢＣの長さって何㎝？

生徒：4㎝

先生：そうだ、1辺4㎝の正方形だからね。ナイス！

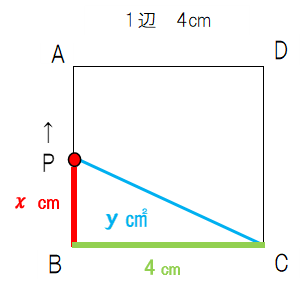
先生：ここまで来ると、三角形の面積ｙを文字式で表すことが出来るね。ｙ＝何？

生徒：y=2x

先生：ナイス、正解だ。三角形の面積は底辺×高さ÷2で出すから底辺と高さに4とｘをあてはめて計算すればいいね。「÷2」は「×1/2」でもいいよ。

先生：ということで y=2x となった。そうしたら（2）の変域の時のｙ＝の式がどうなるか考えよう。点Ｐが辺AD上にある時だ（4≦ｘ≦8）。

先生：この時の底辺BCの長さは？

生徒：4㎝

先生：正解。では高さABの長さは？

生徒：4cm

先生：正解。実は点Ｐが辺ＡＤ上を移動している間、三角形の底辺と高さがずっと同じになっているね。

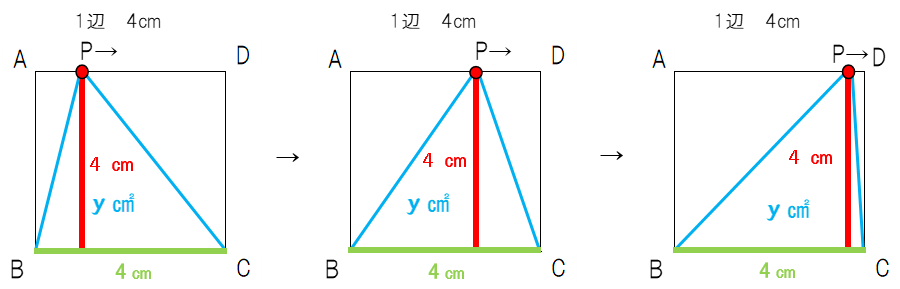
先生：図で左から右に向かって見ていくと、三角形が変形していっても常に緑色の底辺4㎝と赤色の高さ4㎝が同じ長さのままだね。ということは、面積が変わらないままなんだ。この時の面積 y はいくつ？

生徒：ｙ＝8

先生：良く出来ました！面積ｙ＝4×4÷2となって、計算して8と出てくるね。正解！では（3）の変域の時のｙ＝の式がどうなるか考えよう。点Ｐが辺DC上にある時だ（8≦ｘ≦12）。

先生：この時の底辺ＢＣの長さは？

生徒：4㎝

先生：正解。では高さのPCの長さは？これ難しいよ。

・

・

・

先生：どうなった？

生徒：12－ｘ

先生：おお、ナイス正解！DPの長さが出ていないから、1辺4㎝からDPの長さを引いて文字式で表そうとしても出来ないことに気づけたかな。ということで別の長さを出して、そこからPCの長さを出しにいこう。ちなみに3辺分の長さであるBからCまでの長さは何cm？

生徒：12cm

先生：そうだね。以下の図の緑色の部分の長さになるね。

先生：そうしたらBからPまでの長さは？

生徒：ｘ cm

先生：いいね。以下の赤い部分だね。

先生：ということは、以下の図の通り…

先生：ＢからＣまでの長さである12㎝（緑の部分）から余計な長さのｘ㎝（赤の部分）を引けばPC（青い部分）の長さが出てくるんだ。ということでPC＝12－ｘ。これは難しかったね。でも変域の3番目に辺3つ分の長さからｘを引くと三角形の高さ（もしくは底辺）になるパターンがよくあるよ。時間がかかってもいいから頭に染み込ませて理解しておこう。そうすると…

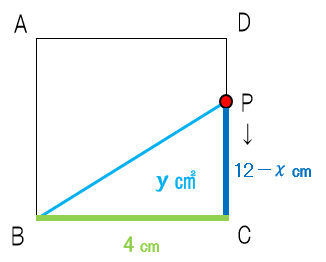
先生：面積ｙ＝の式はどうなる？

生徒：y = 4(12-x)÷2

先生：いいね。計算出来るから計算すると、ｙ＝２(12-x)、更にカッコを外して計算してて順番を整理すると y = -2x+24 となるね。1次関数の式の基本形になるよう変形したよ。

先生：時間がかかったけど、こうしてそれぞの変域でｘとｙの関係がどうなっているのかの式も出すことが出来た。

1－3：グラフを書く

先生：これでグラフを書く準備が整ったよ。ここで問題文、変域と関係式をもう一度確認しておこう。

先生：ここからグラフを書いていこう。まず（1）としてｘの変域が 0≦ｘ≦4 で、式が y=2x のグラフを書こう。以下のグラフ用紙に書いてみて。

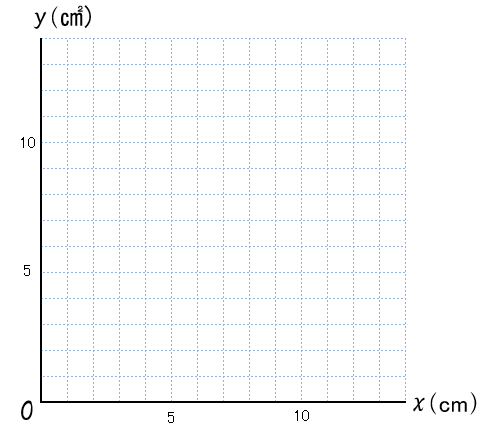
先生：やり方としては、y=2x は切片が0で比例の式になっているからまず(0,0)を通ることがわかる。そしてｘの変域の最大値であるx=4 をy=2x に代入するとy=8が出てくるね。つまり(4,8)を通る直線だとわかるよ。その2点に印をつけてグラフにしよう。そうすると以下の通りになるよ。

先生：このようにグラフが完成したね！

1－4：△ＰＢＣの面積を出す

先生：では次に面積を出しに行こう。問題（2）が残っていたね。

先生：では答えを求めてみて。
・
・
・
先生：答えは何㎠ になった？

生徒：4 ㎠
先生：ナイス、正解！これはいろいろ出し方があるけど、今回はさっき書いたグラフを見ると出しやすい。点Ｐが10㎝移動したということは、ｘ＝10ということだね。

先生：グラフの青丸の部分を見ると「ｘ座標が10の時のｙ座標はいくつなのか？」という状態だね。視線を左の方へ動かそう。その時のｙ座標は4 とわかるね。つまり4 ㎠ だ。

先生：他の出し方もあるよ。x=10ということはｘの変域が（3）8≦ｘ≦12 の時だね。この時の式である y=-2x+24 にx=10を代入すると-20+24=4 と出るね。これで 4 ㎠ と出してもいいよ。これで問題1が解き終わりました。みんなよく頑張りました！

問題2：動点が秒速2cmで動く問題

先生：では2問目の問題に移ろう。2問目は動点が秒速2cmで動くよ。問題は以下の通りだ。まず読んでおいてね。

2－1：変域を表す

先生：この問題も少しずつ一緒に解いていこう。この問題でするべきことは、まずｘの変域を分けて表すことだね。具体的には点Ｐが（1）辺BC上にあるとき、（2）辺CD上にあるとき、（3）辺DA上にあるときの３つになる。それぞれの変域を出して、その後ｘとｙの関係式を作ろう。

先生：では、（1）辺BC上にあるときのｘの変域を出して。どうなった？

生徒：0≦ｘ≦6

先生：ナイス、正解！今回は点Pの速さが秒速2cmだから、6秒で12cm移動してCまで到着するね。ということで動き出した瞬間の0秒後から3秒後までだ。ｘの変域は0以上3以下となる。では次に点Pが（2）辺CD上にあるときのｘの変域を出して。どうなった？

生徒：6≦ｘ≦9

先生：素晴らしい。辺CDの長さが6cmだから、秒速2cmで移動すると移動しきるのに3秒かかるね。ということで、6秒後から3秒たつと9秒後になる。だからｘの変域は6以上9以下となる。では次に点Pが（3）辺DA上にあるときのｘの変域を出して。どうなった？

生徒：9≦ｘ≦15

先生：いいね、正解！（1）と同じように、6秒で12cm移動しきって到着するね。だから9秒後から6秒たつと15秒後になる。そして変域が9以上15以下になる。ということでそれぞれの変域を求めることが出来たわけだ。ここまでまとめると以下の通り。

2－2：変域ごとの関係式を作る

先生：そうしたら次の手順に移ろう。必要な部分の長さを文字式で表す→面積を表す、これをやっていくよ。まずは（1）だけどBPが△ABPの底辺になっているね。そうすると底辺にあたるBPの長さってｘ秒後は何㎝？

生徒：2x (㎝)

先生：正解！

先生：点Pの速さが秒速2cmになっているね。1秒で2cm移動、2秒で4cm移動、3秒で6cm移動する速さだ。秒数の2倍の数字が移動した距離になっているから、ｘ秒後は2xcm移動することがわかるね。では次に三角形の高さを求めよう。何cm？

生徒：6（cm）

先生：その通りだ。長方形のたての長さがそのまま△ABPの高さになっているね。

先生：では面積ｙはどう表せる？

生徒：ｙ＝6ｘ

先生：正解！２ｘと6を掛けて2で割ろう。そうすると6ｘとなるね。ナイス！では（2）辺CD上にあって変域が6≦ｘ≦9の時を見ていこう。

先生：ずばり、ｙ＝いくつ？

生徒：36

先生：正解！点Ｐが辺CD上を移動している間、三角形の底辺と高さがずっと同じになっているね。

先生：底辺AB（青い部分）が6cmで、高さ（緑の部分）が12cmだから、6×12÷2＝36だ。つまり面積 y＝36となる。では（3）の変域の時のｙ＝の式がどうなるか考えよう。点Ｐが辺DA上にある時だ（9≦ｘ≦15）。これは少し難しいパターンだ。式を出してみて。

・

・

・

先生：では聞くけど、どうなった？

生徒：ｙ＝－6x + 90

先生：これは素晴らしい、正解！！これの出し方だけど２つ紹介しよう。まずは普通のパターンだ。

先生：△ABPの底辺をAB（青い部分）とすると、ここは6cmと出ているね。問題は高さのAP（緑の部分）の長さをどう文字式で表すかだ。1問目の（3）の変域のときにやったとおり、ぐるっと回ってきた部分に点Pがあるね。下の図を見てみよう。

先生：この場合はぐるっと回りきった全体（緑部分のBからAまで）から点Pが移動してきた部分（赤部分）を引けばAPの長さが出てくるよ。つまり緑の30から赤の２ｘを引けばいいから、AP＝30－ｘとなるよ。

先生：そうすると、BからC,Dを通ってAまでの長さ（赤＋緑の部分）は30cmだ。そしてｘ秒後のBからC,Dを通ってPまでの長さ（赤い部分）は2xになるんだったね。だからAPの長さは30－2x となる。そうしたら底辺×高さ÷2の式にあてはめよう。6(30-2x)÷2=3(30-2x)=90-6x=-6x+90となるね。つまりｙ＝－6x + 90 となる。

先生：もう１つのやり方を紹介しておくね。ｘの変域が 9≦ｘ≦15 と出ているんだけど、9秒後って点Pはどこになるかな？

生徒：D

先生：そうだね。18cm移動しているからDにあるよね。

先生：ということは面積が6×12÷2＝36(㎠) と出てくるね。これは言い換えると9秒後は36㎠であり、グラフにしたときの座標（9, 36)を通るということだ。次にｘの変域の最大値である15に注目しよう。15秒後は点PがAに到着してしまい、三角形が出来ないから（緑色の部分であるAPの長さが0になるから）面積が0㎠ であることがわかるね。つまり15秒後は0㎠であり、グラフ上で(15, 0)を通るということだ。2点の座標がわかっているから、そこから直線式に直してもいいよ。

2－3：グラフを書く

先生：ここまででグラフを書く準備が出来たね。グラフの問題と各変域に対応する関係式を確認すると以下の通りだ。

先生：ではグラフを３つ繋げて書いてみて。

2－4：面積を求める

先生：では次の問題を解いて行こう。問題を確認したら答えを出してみて。

先生：では聞きます。面積は？

生徒：24 ㎠

先生：いいね。11秒後の面積を求めなさいということは、ｘ＝11のときのｙの値を式に代入して求めなさいということだ。ただしどの変域に当てはまるのかは確認が必要で、3番目の変域 9≦ｘ≦15のところだね。そうしたらその変域の式である y=-6x+90 にｘ＝11を入れて計算しよう。ｙ＝-66 + 90 となって、y= 24 が出てくるね。だから面積は 24 ㎠ だ。

2－5：秒数を求める

先生：では問題2の（3）を解いていこう。問題は以下の通りだから、確認したら解いてみて。

・

・

・

先生：では確認しよう。何秒？

生徒：5秒

先生：あー、おしいね。答えは5秒, 10秒だ。２つあるよ。今回は最初に面積が30と出ていて、逆に何秒たったのか求める問題だね。ということはｙ＝30 のときのｘはいくつなのか探しなさいということだ。

先生：上のグラフを見てみよう。ｙ＝30のところが2か所あるね（青い丸の部分）。そこを下にたどってｘ座標がいくつなのか確認しよう。ここで5秒，10秒というのがわかるね。このようにグラフを見るとみつけやすいよ。試験の問題の多くは整数で出てくるものが多いから、グラフを見て座標を読みとれるなら読み取って答えを書くと早くて正確だ。

先生：ただ問題によってはきちんと計算しないと答えを出せない場合があるから、そのやり方を紹介しておくね。その場合もグラフでざっくりと何秒になるのか確認しておくといいよ。面積30になっているところが左側で見つかるね。そこの変域 0≦ｘ≦6 では式が y=6x だから、それに y=30 を代入しよう。そうすると 30=6x という方程式になって、それを解くと x=5 と出るね。だから5秒後だ。

先生：グラフ上ではもう一か所右側に面積30のところが見つかるから、そこの変域 9≦ｘ≦15では式が y=-6x+90 だね。だからそれにも y=30 を代入しよう。そうすると 30=－6x + 90 という方程式になって、計算すると 6x=60 →両辺を6で割って x=10 と出るね。だから10秒後だ。こうやって計算で答えを出すやり方も出来るようにしておこう。

問題3：動点の移動距離を使う問題Ⅱ

先生：次に問題3を扱うよ。これは問題1の類題になるから、みんなにまず解いてもらおう。問題3と問題4のプリントをダウンロードして、そのうち問題3を解いて下さい。でははじめ！（以下は問題3の解説になりますので、解いたらこのページに戻ってきてくださいね。みなさん正解できますように！）

3－1：変域とグラフ

先生：変域だけど、それぞれ点Pが（1）辺DC上にある　0≦ｘ≦6、（2）辺CB上にある　6≦ｘ≦12、（3）辺BA上にある　12≦ｘ≦18 の3パターンに分ければいいね。それぞれの辺の長さから式を作り、グラフを作っていくと以下の通りになるよ。

（1）点Ｐが辺DC上にある 0≦ｘ≦6

• 三角形の面積を求める式は 底辺6に高さｘを掛けて2で割ると3x になる → 式 y=3x
• ｘの最大値6を式に代入してｙ＝18 → (6, 18)と原点を通る直線をグラフにして書く

 

（2）点Ｐが辺CB上にある 6≦ｘ≦12

• 三角形の面積を求める式は 底辺6に高さ6を掛けて2で割ると18 になる → 式 y=18
• ｘの最大値12の時ｙ＝18 → (12, 18)と先に印をつけた(6, 18)を通る直線をグラフにして書く（ここの変域の時は、ｘがいくつでも面積が18で変わらない＝グラフが水平になる）

（3）点Ｐが辺BA上にある 12≦ｘ≦18

• 三角形の高さとなるAPの長さを出しておこう。上の図のように、APの長さ（右図の青い部分）はぐるっとまわってきたDCBAの長さ18（左図緑の部分）からDPの長さｘ（中央図赤の部分）を引いたものなので、18－ｘとなる。

• 三角形の面積を求める式は 底辺6に高さ18-xを掛けて2で割ると6(18-x)÷2 になる → 式 y=-3x+54
• ｘの最大値18を式に代入してｙ＝0 → (18, 0)と先に印をつけた(12,18)を通る直線をグラフにして書く

3－2：面積を求める

先生：では問題3の（2）の答え合わせと解説だ。

先生：（2）の答えは何になった？

生徒：9 ㎠

先生：ナイス、正解だ！まずグラフを見て読み取れるか確認しよう。

先生：ｘ＝15のところを見て面積を読み取ると、9 ㎠ だと言えそうだね。でも正確でないかもしれないから、計算で出しておこう。ｘの変域が 12≦ｘ≦18 の時の式は y=-3x+54 だったね。この式に x=15 を代入しよう。そうすると-45+54=9 となるね。やっぱり9 ㎠ が答えとして正解だとわかる。

3－3：移動距離を求める

先生：では（3）の答え合わせと解説だ。

先生：（3）の答えは何になった？

生徒：5cm, 13cm

先生：良く出来ました、正解！（3）の問題は面積15が先に出ているから、y=15 の時のｘがいくつになるのかを探すということだね。まずグラフでｙ＝15のところのｘがいくつになっているか確認だ。

先生：そうするとはっきりとはわからないけど、大体ｘ＝5, 13 とわかるね。念のため y=15をそれぞれの変域の式である y=3x と y=-3x+54 に代入して確かめてみよう。

先生：計算した結果、5cm, 13cm で正解したことがわかったね。

問題4：動点が秒速3cmで動く問題

先生：次に問題4を扱うよ。これは問題2の類題なんだ。ということで早速解いてもらおう。はじめ！（以下は問題4の解説になります。解いたらこのページに戻ってきてください。）

• 点Ｐが1秒あたりで3㎝進むので、3秒後にＢに到着する→変数ｘの最大値は3（変域が3まで）
• 三角形の面積を求める式は 底辺18に高さ3ｘを掛けて2で割ると27x になる → 式 y=27x
• ｘの最大値3を式に代入してｙ＝81 → (3, 81)と原点を通る直線をグラフにして書く

（2）点Ｐが辺BC上にある 3≦ｘ≦９

• 点Ｐが1秒あたりで3㎝進むので、18㎝すすむのに6秒かかる。3秒後に6秒を足して、Ｃに到着するのは出発してから9秒後→変数ｘの最大値は9（変域が9まで）
• 三角形の面積を求める式は 底辺18に高さ9を掛けて2で割って 81 になる → 式 y=81（面積が81で変わらない）
• ｘの最大値9の時ｙ＝81 → (9, 81)と先に印をつけた(3, 81)を通る直線をグラフにして書く（この変域では面積が81のまま変わらないので水平な線を引く）

（3）点Ｐが辺CD上にある 9≦ｘ≦12

• 点Ｐが1秒あたりで3㎝進むので、9㎝すすむのに3秒かかる。9秒後に3秒を足して、Dに到着するのは出発してから12秒後→変数ｘの最大値は12（変域が12まで）
• 三角形の面積を求めるためにDPの長さを出しておく必要がある。下の図のようにDPは緑色部分36から赤色部分の3xを引いて 36-3x と表せる。
• 式は 底辺18に高さ36-3xを掛けて2で割って 18(36-3x)÷2 になる → 9(36-3x)=-27x+324 → 式 y=-27x+324
• ｘの最大値12を式に代入してｙ＝0 → (12, 0)と先に印をつけた(9, 81)を通る直線をグラフにして書く

4－2：面積を求めるⅠ

先生：では問題4の（2）の答え合わせと解説だ。

先生：答えを聞こう。面積は？

生徒：54 ㎠

先生：いいね、正解だ。2秒後の面積を求めるのでｘ＝2 のときのｙの値を求めよう。最初の変域 0≦ｘ≦3 のところだね。そうしたらその変域の式である y=27x にｘ＝2 を代入、27×2＝54 だから y= 54 だ。面積は 54 ㎠ 。グラフを見て読み取っても良かったね。

4－3：面積を求めるⅡ

先生：では問題4の（3）の答え合わせと解説だ。

4－4：秒数を求める

先生：では問題4の（4）の答え合わせと解説だ。

先生：何秒になった？

生徒：20/27秒、304/27秒

先生：ナイス、正解！今回のはグラフを見ておよそ1秒後と11秒後とわかるけど、はっきりとは読み取れないね。小数か分数で答えが出るかもしれないことを予想しつつ計算で答えを出しにいこう。y=20 ということだから、最初の変域の式と最後の変域の式に代入してｘを求めよう。

先生：両方分数で出したけど、約分できないのでそのまま答えにしていいよ。つまり 20/27秒、304/27秒が正解だ。最後は割り切れなくて不安になったかもしれないね。でも最後までよく頑張りました！では今日の授業はおしまいです。気を付け、礼！ありがとうございました！！