こんにちは、育伸開発です。
今回の授業では理科の回路図計算問題を解けるようにしていきます。まずは直列回路・並列回路それぞれで電流・電圧・抵抗値をどのように出すのか説明します。その後オームの法則を使った計算で、直列回路・並列回路・複合回路について問題の解き方を説明します。
【中2理科 電気】回路図の電圧・電流・抵抗値を出せるようにする授業(2)オームの法則編
原理・原則を理解した上で練習しながら進めていく授業形式となっています。基礎から無理なく一通りの回路計算問題を解けるように授業を組み立てました。
入試前の復習や定期テスト前の練習用にご利用下さい。回路図記号がわかっている前提になっていますので、あやふやな方はそれらを確認してから授業を受けて下さいね。
目次
電流・電圧・抵抗値の出し方(基本ポイント)
電流・電圧・抵抗値を出すときの基本の考え方は以下の通りです。ここではまだざっと目を通しておく程度で構いません。
- 電流は流れる水の量をイメージして、分かれ道が無ければどこも同じ量である
- 電流が分かれたあとはそれぞれの量を足して合流する
- 電圧は電流を流そうと押す力であり、抵抗のあるところで力を使う
- 電源の電圧を一周したら使い切る
- 電圧は並列部分で一気に同じ力がかかる
- 全体抵抗の値は直列部分では足して求める
- 抵抗値は並列部分では抵抗値の逆数を足して最後に逆数にして求める
では実際に授業を進めていきましょう。今回の授業は1回目ということで、複合回路の電流・電圧・全体抵抗を求めるところまでを扱います。
電流の出し方・基本
先生:では今日の授業をはじめよう。気を付け、礼。お願いします!
生徒:お願いします!
先生:今日は回路図が出てきたときに電流・電圧・抵抗値をそれぞれ出せるようにしていくよ。まずは電流がどれくらい流れているかを出せるようにしよう。電流については流れる水の量をイメージして、分かれ道が無ければどこも同じ量、分かれた後はそれらを足した量が合流する、と考えよう。
単位として覚えておくのは1A(アンペア)=1000mA(ミリアンペア)だということだよ。これは1L=1000mLという液体のかさを表す単位の変換と同じ感覚を使ってね。
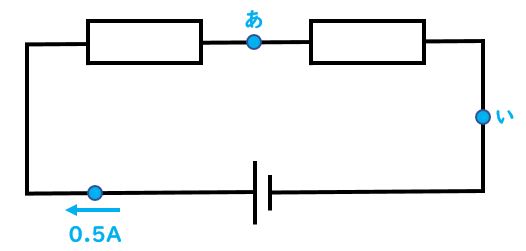
先生:具体的には上の図を見て考えよう。これは分かれ道がないから直列回路になっているね。今左下の青印の部分で電流が0.5A流れているだけど、上の「あ」の部分も同じ0.5Aが流れているんだ。では質問するけど、右側の「い」の部分、ここで流れている電流の量は何A?
生徒:0.5A
先生:そのとおり。分かれ道が無ければどこも同じ量になるから、今回はどこも0.5Aの電流が流れているね。次に下の図を見てみよう。以下の図は途中で回路が分かれているね。だから並列回路になっているんだ。そして左下の部分で電流が0.7A流れているとしよう。
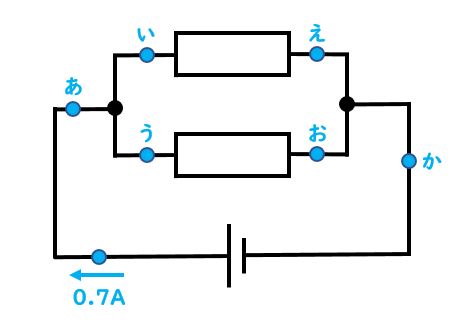
先生:ではこの状態で質問するよ。「あ」の部分で電流は何A流れている?
生徒:0.7A
先生:いいね。まだ回路が分かれていないから、左下の部分と同じ0.7Aの量の電流が流れているんだ。ではここで問題条件を加えよう。以下の図のように「う」の部分を計測したら電流が0.5A流れていたとするよ。
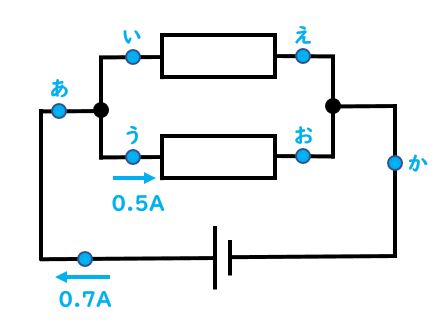 先生:そうすると、「い」部分で電流が何A流れているかわかるかな?…というと、ここは0.2Aになるよ。「あ」の部分までずっと0.7Aの量が流れていて、そのうち0.5Aが下の「う」の方へ流れていったと考えるんだ。だから、残りの0.2Aが上の「い」の方へ流れていったことになるよ。0.7Aから下に流れた0.5Aを引いて0.2Aという計算だ。
先生:そうすると、「い」部分で電流が何A流れているかわかるかな?…というと、ここは0.2Aになるよ。「あ」の部分までずっと0.7Aの量が流れていて、そのうち0.5Aが下の「う」の方へ流れていったと考えるんだ。だから、残りの0.2Aが上の「い」の方へ流れていったことになるよ。0.7Aから下に流れた0.5Aを引いて0.2Aという計算だ。
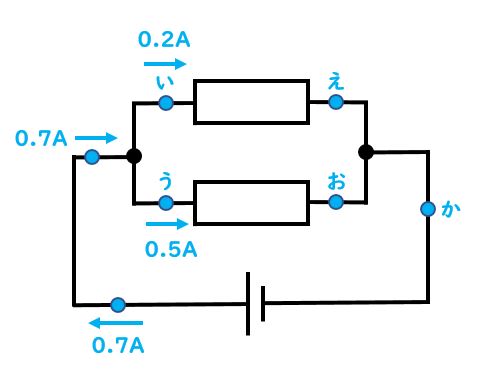 先生:では次に質問。ここまででわかっている電流の量は上の図の状態になっているわけだけど、「え」の部分は何A流れている?
先生:では次に質問。ここまででわかっている電流の量は上の図の状態になっているわけだけど、「え」の部分は何A流れている?
生徒:0.2A
先生:ナイス、正解!では「お」の部分は何A?
生徒:0.5A
先生:いいね、正解だ。「い」から「え」の部分は回路が分かれていないね。だからその間はずっと同じ電流の量になって0.2Aだ。同じように「う」から「お」の部分もずっと0.5Aだ。
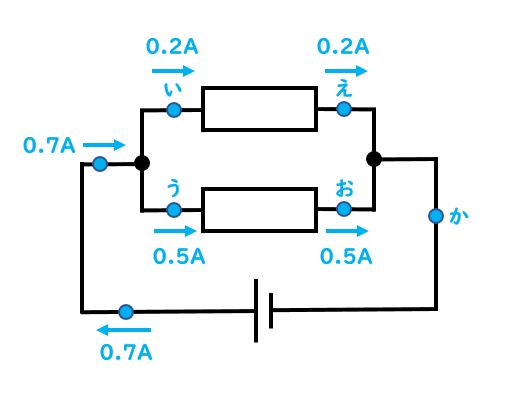 先生:では次の「か」の部分だけど、流れているのは何A?
先生:では次の「か」の部分だけど、流れているのは何A?
生徒:0.7A
先生:素晴らしい、正解!分かれた後はそれらを足した量が合流するわけだから、0.2Aと0.5Aを足して0.7Aとしよう。もちろんその後は分かれ道が無いから0.7A流れているのが電源の部分や最初の左下の部分まで続くよ。
電圧の出し方・基本
先生:では次に電圧がどのようにかかるか見ていこう。電圧というのは電流を流すための押す力のことだ。電源の電圧を抵抗のある所で押す力として使い、一周したら使い切るよ。別の言い方をすると、直列回路では、電源の電圧はそれぞれの抵抗部分で使っている電圧の合計(和)になるよ。これがポイントね。あと電圧の単位はV(ボルト)となる。
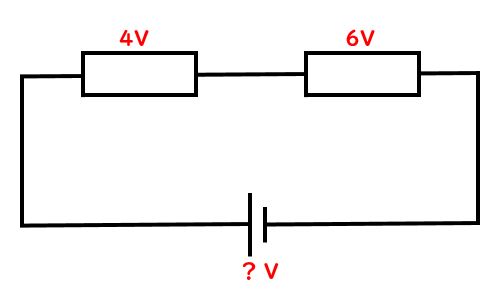
先生:では具体的に直列回路の場合から見ていこう。上の図のように、今抵抗のあるところで4V・6Vと電圧がかかっている。ここで電源の電圧は何Vになっているのだろうか?
先生:…ということで答えを先に言うと10Vだよ。直列回路では、電源の電圧はそれぞれの抵抗部分で使っている電圧の合計(和)になるわけだから、4V+6v=10Vとなる。左上でまず4Vを使い、右上で6Vを使っているから合計すると全部で「10V」ということだ。
先生:では類題を出そう。下図の直列回路で、左上の抵抗の部分でかかっている電圧は何Vになる?今度は聞いてみよう。答えは何V?
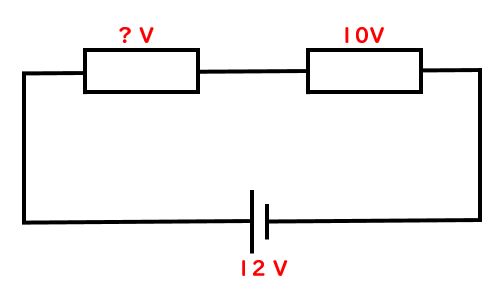
生徒:2V
先生:正解!電源の12Vを一周して使いきるということは「?V」+10V=(電源の)12Vになるということだ。だから、12から10を引いて2Vとなるよ。
先生:次に並列回路の電圧のかかり方を見ていこう。ここでの原則は並列部分では一気に同じ力(電圧)がかかるということだ。単純な並列回路では電圧を一気に一回使って使い切るよ。これを意識しよう。そうすると、下図の並列回路の図で一番上の部分が40Vとなっているけど、その下の所と一番下の電源の部分は何V電圧がかかっているかわかる?
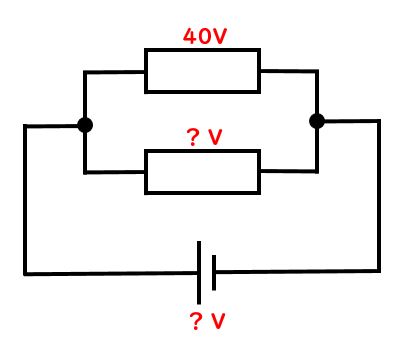
先生:…というと、両方40Vになっているんだ。並列部分では同じ電圧がかかるので、40Vだよ。そして電源の部分の電圧を考えるときも、並列部分で一回だけ一気に40V使って使い切ると考えよう。だから電源も40Vなんだ。
先生:そうしたら類題を出そう。下図の並列回路で電源の電圧が100Vとなっているね。この場合の抵抗がある部分にはそれぞれ何Vの電圧がかかっている?
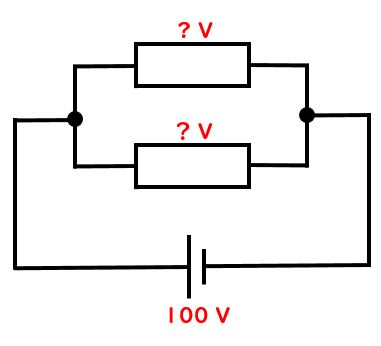
生徒:100Vと100V
先生:いいね、正解!電源の電圧100Vを一周で使い切るわけだけど、並列部分では一気に一回で100Vを使い切るね。そして並列部分では同じ電圧がかかるので、両方100Vだ。100Vを同じ電圧で分けて50Vずつ、なんてやらないように注意しよう。
全体抵抗(合成抵抗)の出し方・基本
先生:そうしたら3番目、全体抵抗の出し方を教えよう。抵抗というのは電流を流しにくくするもののことで、Ω(オーム)という単位で抵抗値を表すものだ。そして回路全体の抵抗を全体抵抗と言うのだけど、それは…
- 直列部分では足して求める
- 並列部分では抵抗値の逆数を足して最後に逆数にして求める
このようにして出すよ。あるまとまり部分を合わせて抵抗値を出したということで、合成抵抗と言ってもいいよ。では具体的に直列回路から見ていこう。以下の図で回路全体の抵抗値は何Ωになるかということだ。聞いてみるけど何Ω?
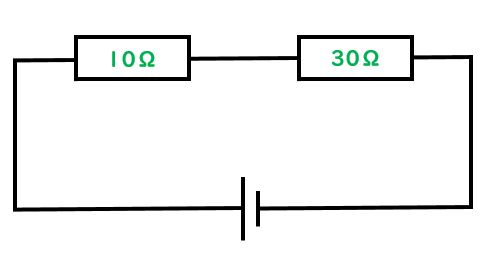
生徒:40Ω
先生:いいね、正解!直列回路だから、10Ωと30Ωを足して40Ωだ。次に並列回路についてやろう。以下の図を見て。並列回路の全体抵抗を出しにいこう。説明すると…
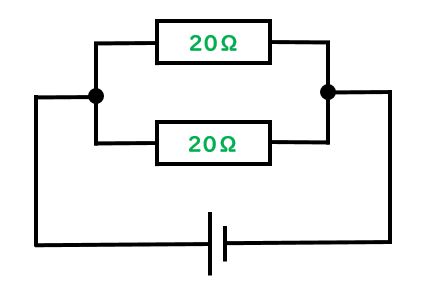
先生:並列回路では抵抗値の逆数を足して最後に逆数にして求める。今回は両方20Ωになっているから、まずその逆数を足すよ。20の逆数は1/20(20分の1)だね(逆数は分母と分子をひっくり返した数字です)。
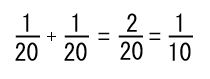
先生:上の図の式のように、1/20と1/20を足すと1/10になるね。最後に1/10を逆数にしよう。その数字にΩ(オーム)を付けると全体抵抗の値になるよ。では全体抵抗は何Ω?
生徒:10Ω
先生:ナイス!今回、20Ωの抵抗を2つ並列させてつなげたら全体抵抗が半分の10Ωになったね。電流を流れにくくしているのが抵抗なんだけど、並列に並べると電流が通る場所が2倍に増えて流れやすくなる、結果全体抵抗が少なくなる、そんなイメージを持っておこう。
先生:では慣れるためにもう1問類題を出すよ。下の図で全体抵抗は何Ωになる?手元で計算してみて。はじめ!
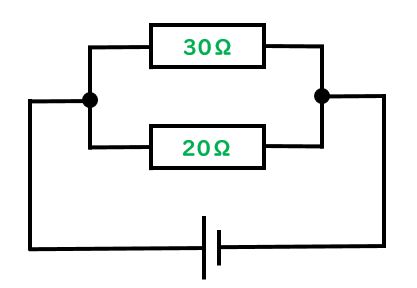
先生:では聞くけど何Ωになった?
生徒:12Ω
先生:正解、素晴らしい!計算式は以下の通りになるよ。
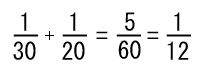
通分計算して約分すると1/12(12分の1)が出てくるね。最後にそれを逆数にするから12Ωだ。
電流・電圧・抵抗値の出し方を復習
先生:ここまでで一通り電流・電圧・抵抗値の出し方を伝えたけど質問ある?
生徒:大丈夫です。
先生:いいね(質問がある方はコメント欄を使って下さい)。最後の全体抵抗を出すのは慣れが必要だけど、個別に見ればそれぞれの出し方はそれほど難しくないね。でもやり方が身についてないと混ぜて問題を出されたときにどう計算すればいいのかわからなくなってしまう。だからここまでの問題をいくつかピックアップして出すから軽く復習しておこう。問題の後少し間を置くから、その間に頭の中で答えを言ってみて。
直列回路の復習
先生:まずは直列回路から。「あ」と「い」の部分の電流を求めよう。
 ・
・
・
・
先生:何A?
生徒:両方0.5A
先生:正解!では以下の回路で電源の電圧を求めて。
 ・
・
・
・
先生:何V?
生徒:10V
先生:正解!では以下の回路で全体抵抗を求めて。

・
・
・
先生:何Ω?
生徒:40Ω
先生:ナーイス、正解!みんなやり方をよく覚えていたね。やり方を間違えたり忘れていたら上の方の授業に戻って説明内容を確認しておいてね。
並列回路の復習
先生:次に並列回路だ。下の図で「あ」「い」「か」の3か所だけ電流を求めて。

・
・
・
先生:「あ」「い」「か」の順に何Aになった?
生徒:0.7A、0.2A、0.7A
先生:正解!では以下の回路の「?」部分の電圧を求めて。

・
・
・
先生:何V?
生徒:両方40V
先生:正解!では以下の回路の全体抵抗を求めて。

・
・
・
先生:何Ω?
生徒:12Ω
先生:素晴らしい、正解!並列回路もみんなよく出来ているね。これらの求め方がごちゃごちゃになっていなければ大丈夫だ。次に進もう。
複合回路
先生:最後に複合回路の問題を解けるようにしていくよ。そして電流・電圧・全体抵抗を出せるようになったら今日の授業は一旦おしまいだ。で、問題を出すから一緒に解いていこう。今までの内容がわかっていればそれほど難しくないから、リラックスして解いていこう。
複合回路の電流
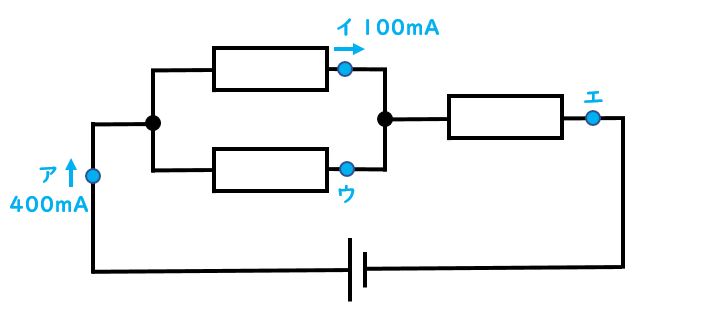
先生:上の図を見て。これが複合回路だ。複合回路というのは直列回路と並列回路が組み合わされている回路のことで、今回の図では左上が並列部分だね。その並列部分と右上の部分は直列に繋がっていると言えるんだ。
先生:では問題を出すよ。ウで流れている電流は何mA?
生徒:300mA
先生:いいね、正解。アの部分で400mAの量が流れていて、それがイとウに分かれていくと考えるんだったね。400mAのうちイに100mA流れたので残りの300mAがウで流れている電流の量になる。400-100=300の計算だ。ちなみに300mAって何Aのこと?
生徒:0.3A
先生:その通り、ナイス。1000mA=1Aが変換基準になっていたね。次の問題。
 先生:上の図でエの部分の電流は何A?
先生:上の図でエの部分の電流は何A?
生徒:0.4A
先生:正解。単位を間違えずに言えたね、ナイス!エからアの部分は回路が分かれていないからずっと同じ電流の量だから、アと同じ400mAがエの部分でも流れていることがわかるね。もしくはイ(100mA)とウ(さっき出した300mA)の合流した後の部分と考えて、100mA+300mA=400mAと考えてもいいよ。ただ、何A?とアンペアの単位で聞いているので、400mA=0.4Aという答えだ。
複合回路の電圧
先生:次は電圧についてやるよ。以下の回路で「?V」となっている並列部分の電圧と、電源の電圧を求めて。
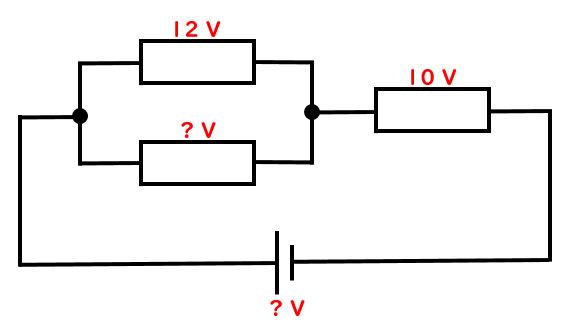
先生:では聞くけど、並列部分の電圧は何V?
生徒:12V
先生:いいね、正解。並列部分では同じ電圧がかかるのだったけどすぐ上に12Vとあるので、下の部分も12Vだ。では電源部分の電圧は何V?
生徒:わかりません。
先生:答えは22Vになるよ。
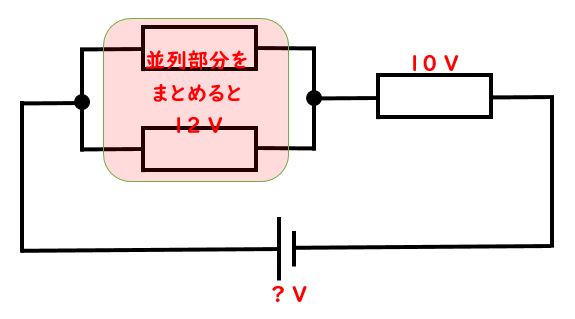
先生:上の図のように、並列部分では12Vの電圧がかかっているね。それはまとめて12Vの電圧が1回かかっているということなんだ。そしてその右側にある10V部分とは直列的につながっているから以下の状態に変換して考えよう。
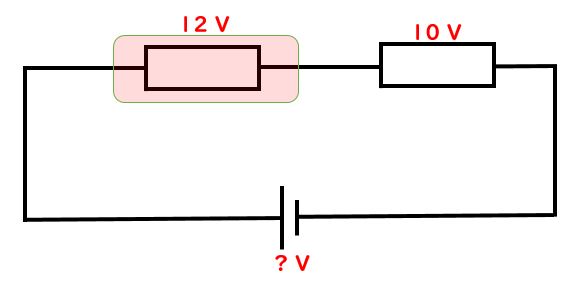
先生:直列につながっている場合、電源の電圧はそれぞれの場所でかかっている電圧の和(合計)になるんだったね。だから12V+10V=22Vとなるよ。
複合回路の全体抵抗
先生:複合回路の最後に全体抵抗を求めよう。以下の図を見て全体抵抗を求めて。ヒントを出しておくけど、さっきの複合回路で全体の電圧を出すのとやり方が似ているよ。
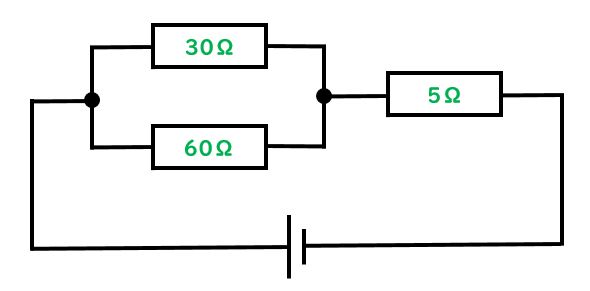
先生:では聞くけど、何Ω?
生徒:25Ω
先生:素晴らしい!まず左上の並列部分の抵抗を出そう。1/30+1/60=3/60=1/20(20分の1)となるね。逆数にすると20になる。ということで、以下の図の通りになるよ。
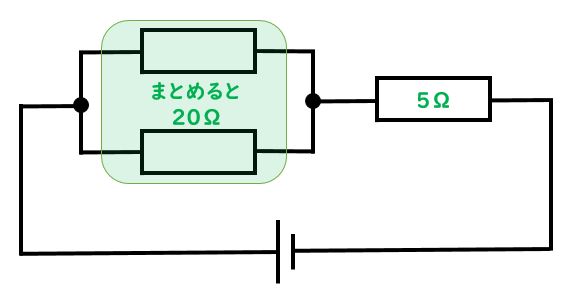 先生:そうしたら直列回路と考えて全体抵抗を20Ω+5Ω=25Ωと出そう。直列回路の全体抵抗はそれぞれの抵抗値の和になるんだった。ここまでで質問ある?
先生:そうしたら直列回路と考えて全体抵抗を20Ω+5Ω=25Ωと出そう。直列回路の全体抵抗はそれぞれの抵抗値の和になるんだった。ここまでで質問ある?
生徒:ありません。
先生:いいね、わかってくれたようで(質問がある方はコメント欄を使って下さいね)。では今日の授業はここまでです。次回はオームの法則を紹介して、その法則を使って計算して数値を求める問題を解けるようにしていくよ。では~気を付け、礼。ありがとうございました^^
いかがでしたか。以下の授業に続きます。ではまた!
【中2理科 電気】回路図の電圧・電流・抵抗値を出せるようにする授業(2)オームの法則編