【算数・数学や理科で使える便利な技】比例関係が成り立つ時に使えるようにしておきたい問題整理方法（２）

こんにちは、育伸開発です。前回の記事「【算数・数学や理科で使える便利な技】比例関係が成り立つ時に使えるようにしておきたい問題整理方法（１）」で比例関係を図式化する方法を紹介しました。今回はそのつづきの内容になります。

生徒は難しい問題でも手を使って書きながら解くことをほぼしませんから、それを出来るようにすることに意味があります。特に使えるのが以下のように即座に何倍かが出ないケースです。

何倍なのか、すぐに判断出来ない問題の例

どうでしょう。こういったケースでは、すぐに何倍かがわかりませんから手が止まってしまう生徒の割合がいきなり大きくなります。すぐに3/8倍であることを出して答えまで出せる生徒は優秀です。

問題文もあえて混乱しやすいものにしてあります。基準を紹介する部分では先に400円という金額が出て、その後に8mという長さが出ています。答えを問う部分では先に3mという長さが来て金額（値段）はいくらかというのが後に出ています。

小6では分数の割り算を学習します。そうすると数値が全て分数になっている問題が出てきます。そして割れば良いのか掛ければ良いのか、優秀な生徒でも感覚的な判断を行うことが出来ないまま解くことになります。優秀な生徒でも60点くらいしか取れないテストになる単元です。

問題に戻りますね。こうなると生徒は以下のやり方を始めることがあります。

割り算の勉強をしているから割り算の式を立ててみよう。長さが8mと3mと出ているから8÷3だな（大きい数を小さい数で割ろうとする傾向があります）。あれ？割り切れないぞ？→手が止まる。（このやり方、全く考えていない解き方です。式や答えが合っていても、たまたまなだけですね。）

割り切れなくても式が出ていればとにかくやってみる生徒も数多くいます。

8÷3＝8/3（3分の8）だな。そうしたら、400×8/3をしてみよう。計算すると・・・3200/3円。先生、3200/3円になった！←よく頑張りました。でも不正解です。こんなことが実際に起こり得ます。

どうすれば良いのか

では、そういったことを生徒が始めたり、わからないから止まっている時にどう指導したらよいか紹介します。前提として、何倍かがわからない時は割り算で求める、割り算は「分子÷分母」の関係で分数にする、「同じ数÷同じ数＝1」である、これらのことを知っているものとします。

ここからは授業風でお届けいたします。生徒を指導する方や子供に教える保護者の方、ご参考下さい。

生徒：先生、わかりません。

先生：これ難しいよね。解説入れるよ。

生徒：はい。

先生：まず確認だけど、この問題では3mで何円なのかを聞いているよね。ということはそれを求めるための基準が書いてあるはずだ。何mで何円って書いてある？

生徒：8mで400円。

先生：その通り！書くとこうなるね。で、さっき確認したとおり、尋ねられているのは3mで何円かだから、それも書くとこうなるね。

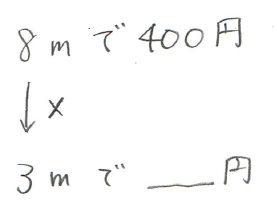
先生：ここまでいいかな？

生徒：はい。

先生：そうすると、両方の数字が出ているのは左側だね。で、ここが難しいのだけど、8mを3mにするのって何倍か出せそう？

生徒：わかりません。

先生：だよね。こういう何倍かがわからないときは、逆に割り算をするんだ。今回は3÷8で3/8（8分の3）だ。

つまり、×3/8ということがわかるよ。ここまで大丈夫？

生徒：大丈夫です。

先生：いいね。そうするとこっちの400という数字もどうしなければいけないかな？

生徒：3/8×

先生：あ、これは「3/8×」ではなくて、「×3/8」だよ。（必要に応じて「3/8×」にしてしまうと、答えを出す式が「400 3/8×＝」とおかしくなってしまうね、と説明します。）そうしたらあとは計算するだけだ。

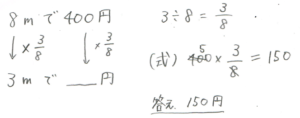
先生：こうやって計算すると150が出てくるね。すなわち答えが150円となるんだ。わかった？

生徒：わかりました。

先生：じゃぁこの解説メモじっくり見て吸収して。その後もう一回解いてみよう。そのときにこの技を使って書きながら式を見つけていくようにね。

いかがでしょうか。このように解説授業を進めていきます。

各学年で扱っている学習内容

ちなみに、何倍かを出す割り算計算は小学校4年生で学習します。小学校5年生では小数の割り算の解き方を学習しますが、その後でやはり何倍なのか出すやり方を小数版で学習します。また小学校5年生の最後で割る数が分数の分母に掛け算で入ることを学習します。そして小学校6年生では分数の割り算を学習するときに、分数版で何倍なのかを出すやり方を学習します。

このように何倍なのかを出すやり方は高学年で繰り返し出てくるのですが、逆に割って出すというやり方は定着していないケースが多いです。また小6以降の話ですが、自然数の割り算を「分子÷分母」と見て分数にすることをいきなり正解させるのは難しいです。そのため事前にその変換だけについてやり方を教えておくとスムーズです。

認識させたいこと

あと、指導をする上で注意点があります。それはどういう計算をしてるか聞いたときに「×３」や「÷５」などと加減乗除の記号の後に数字が来るよう言わせることです。3倍にすることを式にすると「×3」であり、5つに分けたり5等分することは「÷5」なのです。これを「3×」や「5÷」と言うことは間違いです。授業風の解説途中で生徒が「3/8×（8分の3掛ける）」と言っていましたが、そう言ってしまうことがしばしばあります。

少し哲学的な感じになってしまいましたが、勉強な苦手な生徒はどのような計算操作をしているのか正しく言えない傾向があるのです。別の言い方をすると、「３×」や「５÷」と最初の数字と次の記号を固まりとして見てしまっているのです。「５×・・・」だと５に何を掛けるのか数字が出ていませんから計算出来ません。３を5倍するということは３（の右）に「×５」の式を追加することですが、これを認識させて正しく言えるように必要があります。

つづく