【中3数学 2次関数】動点とグラフの問題について丁寧な解説がたくさんある授業

こんにちは、育伸開発です。

今回は2次関数・動点とグラフの問題を扱います。中2で出てくる1次関数の動点問題の続き内容で中3版になります。

多くの生徒が苦手とするものですが、中2内容・中3内容をそれぞれトレーニングしておけばクリア出来ます。

「よし、頑張ろう」

そんな気持ちをお持ちのみなさんに向けて後押しするための授業を用意しました。頑張るみなさんを応援します！

動点の文章問題を解く時の手順

動点の問題を解くには手順が4つあります。まずはサラッと確認しておいて下さい。具体的には問題を解いていくことで何を意味しているのかわかるようになります。

1. ｘの変域を分けて表す
2. 必要な部分の長さを文字式で表す
3. 文字式で面積を表す
4. 変域から座標を出してグラフにする

では模擬授業を始めます。

問題1：変域が1パターンのタイプ

先生：では授業をはじめます。気をつけ、礼。お願いします！今日は数学の2次関数の応用問題を扱っていくよ。動点の問題だ。

生徒：2次方程式のところでやったやつですよね。

先生：そうだね。あと、中2の1次関数のところでも出てきていたね。今回もじっくり解説しながら授業を進めていくからね。まず手順を4つ紹介しよう。

1. ｘの変域を分けて表す
2. 必要な部分の長さを文字式で表す
3. 文字式で面積を表す
4. 変域から座標を出してグラフにする

先生：この通りにやっていけば答えを出せるようになるよ。では早速問題を1つ出すから、一緒に解いて行こう。

 

1－1：xの変域を表す

先生：そうしたら、まずｘの変域を表そう。具体的には点Ｐと点Ｑが進みきるとそれ以上動けなくなるね。何秒でそうなるのか確かめてみよう。では聞くけど、点Ｐは何秒でＡに到着する？

生徒：10秒

先生：いいね。ACの長さが10㎝になっているから、秒速1㎝の速さで進むと10秒で進みきるね。では点Qは何秒でＢに到着する？

生徒：10秒

先生：ナイス！BCの長さが20㎝になっているから、秒速2㎝の速さで進むと同じく10秒で進みきるね。ということでｘの変域の最大値が10（秒）とわかったね。すなわちｘの変域は 0≦ｘ≦10 ということだ。その後特に別の辺の上を移動するわけではないので、変域をいくつかに分けて考える必要無いね。今回は変域は1パターンだけで、式も１つだけになるということだ。その確認が出来たところで(1)の問題を解きに行くよ。

1－2：文字式で面積を表す

先生：そうしたら次の手順として、必要な部分を文字式で表そう。

先生：今このような図の状態だね。三角形の面積ｙを表すように問題で指示されているから、三角形の底辺と高さに当たる部分を文字式で表そう。そうするとｘ秒後のCPの長さは？

生徒：x (cm)

先生：いいね。1秒で1㎝進む速さだからｘ秒でｘ㎝進むことになるね。秒数と何㎝進んだかの部分が同じになるよ。そうしたらCQの長さは？

生徒：2x (cm)

先生：ナイス、正解！点Qが1秒で2㎝進む速さだからｘ秒で2ｘ㎝進むことになるね。秒数の2倍が何㎝進んだかになるよ。そして以下のように図の長さを表すことが出来た。

先生：そうしたら面積y をｘの式で表そう。(1)の答えはどうなる？

生徒：

先生：その通り、正解。

 

 

 

先生：三角形の面積の公式は「底辺×高さ÷2」だ。だから底辺の２ｘ（青）と高さのｘ（赤）を掛けて2で割ればいいね。÷2 の代わりに ×1/2 にしてもいいよ。では次、(2)の問題を解こう。

先生：これ、解いてみて。

・

・

・

先生：では答えを確認するよ。どうなった？

生徒：0≦ｘ≦10，0≦ｙ≦100

先生：素晴らしい、正解！ｘの変域はすでに最初に出していたとおりで、10秒後に点が両方とも最後まで進みきってしまうんだったね。あとはｘの変域の最低値0と最大値10をさっき出した以下の式に代入しよう。

 

 

先生：そうすると、ｘ＝0の時ｙ=0、ｘ＝10の時ｙ=100だ。ということで(2)の答えは 0≦ｘ≦10，0≦ｙ≦100 だ。

1－3：面積から時間を求める

先生：次に(3)を解こう。

先生：これを解いていくのだけど、まず△ABCの4分の1の面積を出しておこう。いくつになる？

生徒：25（㎠）

先生：正解！三角形の面積が20×10÷2＝100（㎠）と出ているから、100を4分の1にして25（㎠）と出てくるね。そうすると(3)の問題が解けるようになった。動き出してから何秒後？

生徒：5秒後

先生：良く出来ました！今回はｘとｙの関係式が以下のようになっているね。

 

 

先生：今回は面積ｙが25（㎠）とすでに出ているから、ｙに25を代入して以下の方程式を解こう。

 

 

先生：これを解いてｘ＝±5 だ。x=5というのは5秒後ということで、x=-5のほうは-5秒後ということだ。ただし-5秒後というのは問題の意図より不適格だとわかるので（5秒前ということで、まだ点が動いていないのにおかしい）、ｘ＝5 だね。すなわち答えは5秒後となる。

1－4：問題1の答え（まとめ）

まとめると問題1の答えは以下の通り。

(1)

(2) 0≦ｘ≦10，0≦ｙ≦100

(3) 5秒後

問題2：変域が別れるタイプ

先生：では次の問題を解いていこう。レベルアップして少し複雑になるよ。

2－1：AD上にある時の変域と式

先生：では(1)を解いていこう。まずは変域の確認から。ｘの変域はどうなる？

生徒：0≦ｘ≦4

先生：その通り。正方形の1辺の長さが4㎝で点Ｐが1秒で1㎝移動するから4秒でDに到着するね。ということで最初から４秒後までの変域を表すと0≦ｘ≦4 だ。その時のｙを表した式は？

生徒：

 

 

先生：素晴らしい、正解！今回は点Ｐも点Ｑも秒速１㎝で同時に動き始めるから、ｘ秒後の移動距離はｘ（㎝）になるね。以下の図の通りだ。

先生：そうすると面積ｙは底辺ｘと高さｘを掛けて２で割れば出てくる。以下のように式が出てくるね。

 

 

2－2：DC上にある時の変域と式

先生：では(2)に移るよ。問題を再掲しておこう。

 

先生：今回はｘの変域と式を出してもらおう。少し時間をあげるから答えを出してみて。

・

・

・

先生：では確認するよ。答えはどうなった？

生徒：4≦ｘ≦8, y=8

先生：いいね、正解！

変域だけど、１辺４㎝を移動するのに秒速１㎝だと4秒かかかることがわかる。だから点が動き出してから４秒後（今回の変域の最初）に4秒を足して8秒後までの変域となる。4≦ｘ≦8 だね。そしてこの変域の時だけど、面積が一定になるね。

先生：上の図にあるとおり、点ＰがＤから真下に移動している間は点ＱがＢに到着しているから止まっている。そしてずっと底辺が4㎝（青い部分）、高さも4㎝（緑の部分）で変わらないね。だから4×4÷2＝8となる。面積は 8㎠ のままだとわかるんだ。ということで式は y=8 。

2－3：CB上にある時の変域と式

先生：では(3)に移るよ。問題を再掲しておこう。

先生：今回のは式を出すのが難しくなっているんだけど、変域と式を出しみて。少し時間をあげよう。

・

・

・

先生：では確認。答えは？

生徒：8≦ｘ≦12, y=－2ｘ+ 24

先生：おお、素晴らしい。正解！変域だけど、１辺４㎝を移動するのに4秒かかかることがわかっているね。だから点が動き出してから8秒後に4秒を足して12秒後までの変域となる。8≦ｘ≦12 だね。そしてこの変域の時だけど、三角形の高さを出すのが難しいんだ。図を見てみよう。

先生：今点Ｐがぐるっと回ってきて最後の辺を左に向かって移動しているところだ。この時、三角形の底辺であるＰＱの長さを文字式で表したいのだけど、これが12－ｘ（㎝）となるんだ。図からわかるかな？

生徒：わからないです。

先生：この図からだとわかりにくいね。点が辺を移動していってぐるっと回るときは、以下の図のように全体の長さから移動してきた距離を引くと出てくるよ。

先生：全体の長さとは緑の部分で、ＡからＤ，Ｃ、Ｑ（Ｂ）までぐるっと3辺分の長さを足したものなんだ。1辺4㎝だから、3辺分の長さは12㎝になるね。そこから余計なｘ㎝を引くよ。

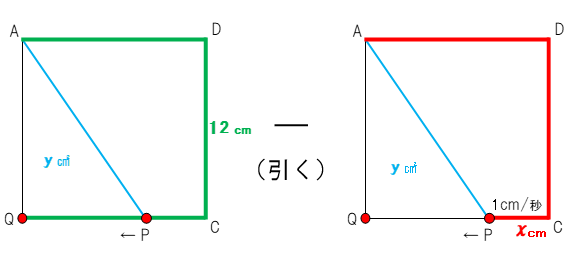
先生：緑の部分（12㎝）から赤の部分（ｘ㎝）を引こう。そうするとPQが 12-x (㎝）と出てくるね（下の図のピンクの部分）。これで準備が整った。

先生：底辺の12－ｘ（ピンクの部分）に高さの4（青の部分）を掛けて2で割ろう。そうするとｙ＝4(12-x)÷2 となって、式を整えると y=－2ｘ+ 24 だ。ということで(3)の答えが8≦ｘ≦12, y=－2ｘ+ 24 となる。

2－4：グラフを書く

先生：では(4)だ。問題を再掲しておこう。

先生：これなんだけど、変域ごとに分けてグラフを書けばいいよ。その時に座標を先に打つとやりやすいからね。では出来る限りでいいので、グラフを作ってみて。

・

・

・

先生：できたかな？答えは以下の通りだ。

先生：前に中2の時にやった1次関数とグラフの問題に慣れている人はやれたかもしれないけど、初めての人には難しかっただろうね。ということで解説を入れていこう。今、(1)から(3)までの問題を解いたから、それぞれの変域に対して式がどうなっているのか全てわかっている状態だ。それをまとめると以下の通りだ。

先生：そうすると、それぞれの変域ごとにグラフを書いていこう。まず(1)の式にｘの変域の最低値である0 を代入しよう。そうするとy=0 となって(0,0)を通ることがわかる。そしてｘの変域の最大値であるx=4 を代入するとy=8が出てくるね。つまり(4,8)を通る放物線だとわかるよ。その2点に印をつけてグラフにしよう。念のため途中のｘ＝2も代入してｙ＝２、すなわち(2, 2)も印をつけておけば試験でバツにされることはないよ。

先生：（2）のグラフはｘの変域が 4≦ｘ≦8 で、式が y=8 だ。ｘの変域の最小値4 の時の面積は8だから、（4,8)に印を打つ…というよりは、さっきの(4,8)と重なるね。もう１つはｘの変域の最大値8の時の面積も8ということで(8,8）に 印を打つ。この変域では面積がずっと8で一定だから、水平な直線で結ぼう。そうすると以下のグラフが追加されるよ。

先生：（3）のグラフはｘの変域が 8≦ｘ≦12 で、式が y=-2x+24 だ。ｘの変域の最小値8 の時の（8,8)はすでに打ってあるから最後の点を探そう。ｘの変域の最大値12の時、ｘ＝12を y=-2x+24に代入しよう。面積y が0になるので(12,0）に 印を打つ。y=-2x+24 の式は1次関数の直線式になっているね。だから（8,8)と(12,0）を直線で結ぼう。そして以下のグラフが追加されて完成だ。

2－5：何秒後なのかを出す

先生：(5)だ。問題を再掲しておこう。少し時間をあげるから解いてみて。

・

・

・

先生：では確認しよう。答えは？

生徒：2秒後と11秒後

先生：いいね、正解！今回のはグラフを見るとちょうど整数で答えが見つかるよ。

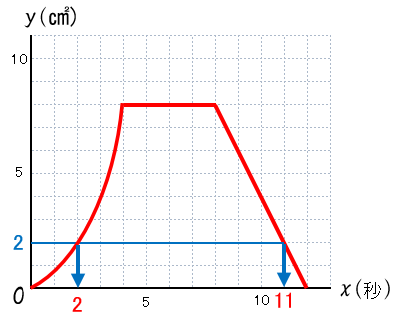
先生：グラフの面積2の部分（青の部分）横に右に向かって見ていこう。そうすると面積2の部分は2か所見つかるね。それを下に見ていくと、ちょうと2秒後と11秒後だと読み取れるんだ。今回はこれが早くて確実な出し方になっている。ただグラフから正確な数字を読み取れない場合、それぞれの変域の式にｙ＝2 を代入してｘの値を計算で出すようにしよう。後で出てくる問題4にそのパターンがあるよ。ということで(5)の答えは2秒後と11秒後。

2－6：問題2の答え（まとめ）

先生：まとめると問題2の答えは以下の通り。

(1) 0≦ｘ≦4

 

 

(2) 4≦ｘ≦8, y=8

(3) 8≦ｘ≦12, y=－2ｘ+ 24

(4)

 

 

 

 

 

 

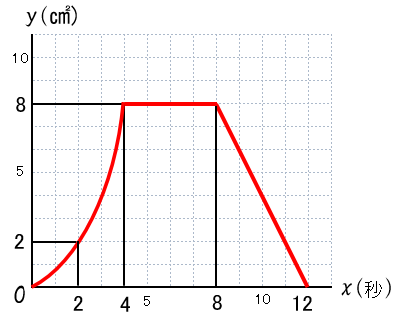
(5) 2秒後, 11秒後

問題3：問題1の類題

先生：では問題3をやろう。問題3はすでに解いた問題1の類題だよ。同じパターンにしてあるから、さっき勉強したことを参考にしてね。(1)から(3)まであるので、プリントをダウンロードして解いてみて下さい。解いたら解説授業を始めるからここに戻ってきて下さいね。では始め！

3－1：ｙを表す式

先生：では答え合わせと解説をしよう。(1)の答え何になった？

生徒：

 

 

先生：いいね、正解！1/8のところは0.125でもいいよ。以下の図のようにｘ秒後のAPとAQの長さが0.5ｘと表せるね。

先生：そうすると面積ｙは底辺の0.5ｘと高さの0.5ｘを掛けてさらに×1/2をしよう。

 

 

になる。比例定数の部分だけど、1/2を3回かけることになるので1/8でも同じことだね。

3－2：ｘとｙの変域

先生：では(2)の答えを合わせよう。「ｘの変域とｙの変域を求めなさい」とあったけど、何になった？

生徒：0≦ｘ≦4, 0≦ｙ≦2

先生：その通り！まずｘの変域だけと、1辺２cmを秒速0.5cmで進むとあるから、2÷0.5＝4としよう。4秒で進みきるから最大値が4とわかる。そうしたらｘの最大値4を(1)で出した式に代入して 1/8×16＝2 と出そう。すなわちそれがｙの最大値だ。ということで答えは 0≦ｘ≦4, 0≦ｙ≦2 。

3－3：何秒後なのかを出す

先生：では(3)について。「△AQPの面積が正方形ABCDの2分の1になるのは点Pと点Qが動き出してから何秒後ですか」と聞いてあったけど、答えは？

生徒：4秒後

先生：素晴らしい、正解！面積が正方形の面積が2×2＝4㎠ となっていて、その2分の1の面積は2㎠だね。ということで(1)で出した式の面積ｙに2を代入すると以下のようにｘについての方程式が出来る。

 

 

先生：そうしたらこれを解いてｘ＝±4 だ。ただしｘ＝－4は問題の意図より不適格だね。－4秒後というのは有り得ない。すなわちｘ＝4 となるから答えは4秒後だ。

3－4：問題3の答え（まとめ）

まとめると問題3の答えは以下の通り。

(1)

 

 

(2) 0≦ｘ≦4, 0≦ｙ≦2

(3) 4秒後

問題4：問題2の類題

先生：問題4だ。これは解いた問題2の類題だよ。(1)から(5)まであるので、プリントをダウンロードして解いてみて下さい。解いたら解説授業を始めるからここに戻ってきて下さいね。では始め！

4－1：CB上にある時の変域と式

先生：では(1)を解いていこう。まずは変域の確認から。ｘの変域はどうなる？

生徒：0≦ｘ≦4

先生：その通り。長方形の縦の長さが4㎝で点Qが1秒で1㎝移動するから4秒でDに到着するね。横の長さは8㎝で点Pが1秒で2㎝移動するから、点Qと同じ4秒でBに到着するね。ということで最初から４秒後までの変域を表すと0≦ｘ≦4 だ。その時のｙを表した式は？

生徒：

 

 

先生：ナイス、正解！以下の図のように、底辺が２ｘ、高さがｘと表すことが出来るね。

先生：２ｘ（赤の部分）とｘ（青の部分）を掛けて更に1/2を掛けよう。計算すると式が出てきて以下が答えだ。

 

 

4－2：BA上にある時の変域と式

先生：では(2)に移るよ。問題を再掲しておこう。

先生：(2)の答えは何になった？

生徒：4≦ｘ≦6, ｙ＝16

先生：グッジョブ、正解だ。変域だけど、長方形の縦の長さ４㎝を移動するのに2秒かかかる。だから点が動き出してから4秒後（今回の変域の最初）に2秒を足して6秒後までの変域となる。8≦ｘ≦12 だね。

先生：そしてこの変域の時、面積が一定になるね。上の図にあるとおり、点ＰがBから真上に移動している間はすでに点ＱがDに到着して止まっている。そしてずっと底辺が4㎝（青い部分）、高さが8㎝（ピンクの部分）で変わらないね。だから4×8÷2＝16となる。面積は 16㎠ のまま一定だ。ということで式は y=16 。

4－3：AD上にある時の変域と式

先生：では(3)だ。問題を再掲しておこう。

先生：(3)の答えは何になった？

生徒：6≦ｘ≦10, ｙ＝－4ｘ＋40

先生：よく出来たね、正解！変域だけど、横の長さ8㎝を移動するのに4秒かかかることがわかるね（8÷2=4）。だから点が動き出してから6秒後（変域の最初）に4秒を足して10秒後までの変域となる。6≦ｘ≦10 だね。そしてこの変域の時だけど、三角形の高さを出すのが難しいパターンだった。以下の図を見よう。

先生：今点Ｐがぐるっと回ってきて最後の辺を右に向かって移動しているところだ。点Pが移動してきた距離が全部で 2x（cm）となっているね（赤の部分）。そして△QPCの底辺はQCで高さがPQだとしよう。この時、三角形の高さであるＰＱの長さを文字式で表したいのだけど、これが 20－2ｘ（㎝）となるんだ。

先生：その出し方を説明しよう。点が辺を移動していってぐるっと回るときは、以下の図のように全体の長さから移動してきた距離を引くと出てくるのだったね。全体の長さとは緑の部分で、ＣからＢ，Ａ、Ｑ（Ｄ）までぐるっと3辺分の長さを足したものなんだ。3辺分の長さは8+4+8で20㎝になるね。そこから余計な2ｘ㎝を引くよ。

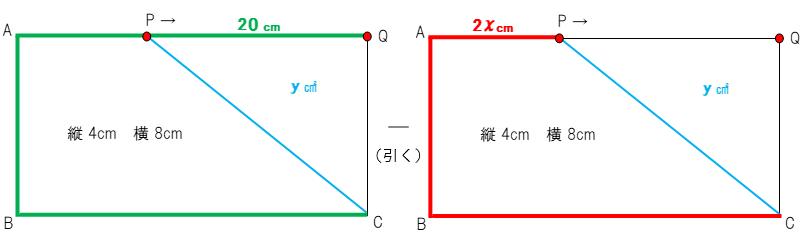
先生：緑の部分（20 ㎝）から赤の部分（2x ㎝）を引こう。そうするとPQが 20-2x (㎝）と出てくるね（下の図のピンクの部分）。これで準備が整った。

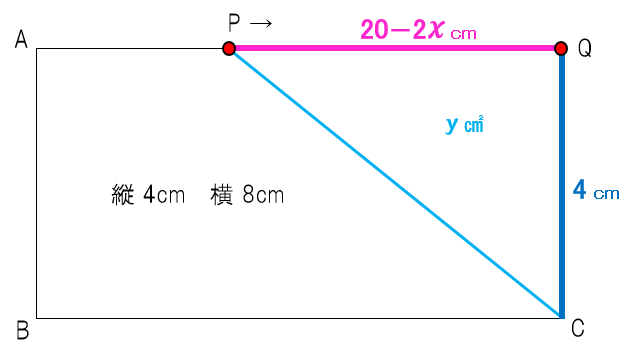
先生：底辺の4（青の部分）に高さの20－2ｘ（ピンクの部分）を掛けて2で割ろう。そうするとｙ＝4(20-2x)÷2 となって、式を整えると y=－4ｘ+ 40 だ。ということで(3)の答えが 6≦ｘ≦10, ｙ＝－4ｘ＋40 となる。

4－4：グラフを書く

先生：では(4)だ。問題を再掲しておこう。

先生：答えは以下の通りだ。

先生：では解説を入れていこう。(1)から(3)までの答えからそれぞれの変域に対して式がどうなっているのかまとめると以下の通りだ。

先生：ではそれぞれの変域ごとにグラフを書いていこう。

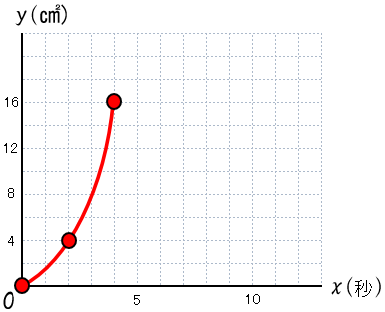
先生：まず(1)の式にｘの変域の最低値である0 を代入、そうするとy=0だ。(0,0)を通ることがわかる。そしてｘの変域の最大値であるx=4 を代入するとy=16が出て(4,16)を通る放物線だとわかる。その2点に印をつけてグラフにしよう。途中のｘ＝2も代入してｙ＝２、すなわち(2, 2)も印をつけておくよ。

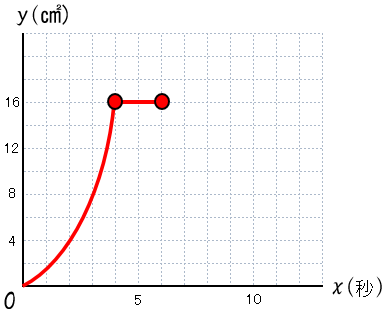
先生：（2）のグラフはｘの変域が 4≦ｘ≦6 で、式が y=16 だ。ｘの変域の最小値4 の時はさっきの(4,16)と重なるのだったね。もう１つはｘの変域の最大値6の時の面積も16ということで(6,16）に 印を打つ。この変域では面積がずっと16で一定だから、水平な直線で結ぼう。

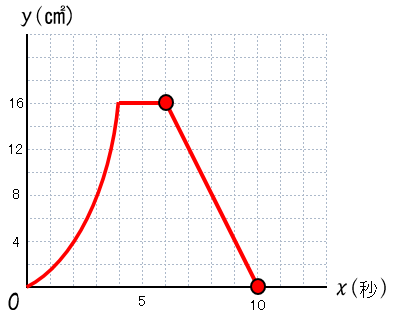
先生：（3）のグラフはｘの変域が 6≦ｘ≦10 で、式が y=-4x+40 だ。ｘの変域の最小値6 の時の（6,16)はすでに打ってある。最後の点はｘの変域の最大値12の時で、ｘ＝10を y=-4x+40に代入しよう。面積y が0になるので(10,0）に 印を打つ。y=-4x+40 の式は1次関数の直線式になっているね。だから（6,16)と(10,0）を直線で結ぼう。そして完成だ。

4－5：何秒後なのかを出す

先生：最後の(5)だ。問題を再掲しておくよ。

先生：では確認しよう。答えは？

生徒：8.5秒後

先生：おしいね、半分正解だ。正しい答えは以下の通り。

 

 

先生：今回のはグラフを見ると面積が 6になるときのｘが2か所あることがわかる。それぞれ 2.5と8.5くらいだ。でもはっきりとはわからないね。

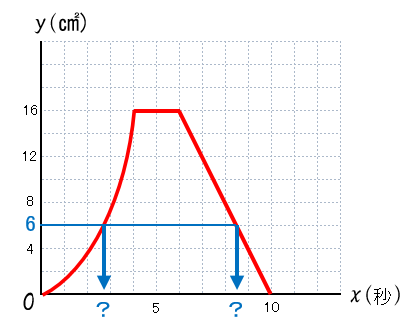
先生：そういうときはそれぞれの変域の式にｙの値6 を代入して計算しよう。(1)の式にｙ＝6を代入すると

 

 

となるね。あとはこの方程式を解いて解を出そう。

 

 

ー√６（マイナスルート6）だけど、マイナスになっているので題意より不適格な数だ。＋√6（プラスルート6）だけど、これは2.4くらいの数字だから問題ないね。答えの1つ目が出た。

先生：次に(3)の変域の式(y=-4x+40)にy=6 を代入しよう。そうすると 6=-4x+40 となって、この方程式を解くとｘ＝8.5 と出る。分数で出した人は17/2（秒後） でもいいよ。この数は問題ないから答えの2つ目にする。ということで

 

 

4－6：問題4の答え（まとめ）

先生：まとめると問題4の答えは以下の通り。

(1) 0≦ｘ≦4

 

 

(2) 4≦ｘ≦6, y=16

(3) 6≦ｘ≦10, y=－4ｘ+ 40

(4)

 

 

 

 

 

 

(5)

 

 

先生：これで4問全て解いたね。みんなお疲れ様でした。宿題出すよ。今日の4問を次回の授業で確認テストとして出すから解けるようにしておくこと。おしまいです。気をつけ、礼。ありがとうございました！

 

今回の授業はいかがでしたか。わかりにくいところがあればコメント欄を使って質問してくださいね。ではまた！