こんにちは、育伸開発です。
今回は中3で学習する2次方程式の応用・動点の問題の授業を行います。点が動いていく状況を把握しつつ方程式を作っていくのがやっかいなものです。実際多くの生徒がこのタイプの問題に苦手意識を持っています。
でも大丈夫です。動点の問題には決まったパターンがありますから、それを押さえて手順どおりに作業を進めれば解けます。何問か解いて慣れれば解く力が付くのです。
復習できるようダウンロードできるプリントも用意しました。定期テストや来たる高校入試に向けて頑張るみなさんを応援します。ファイトー!
今回のダウンロード問題は全部で4問あります。数学が得意な方は先に問題を解いて、後から以下の解説授業を読んでいただいても構いません。
動点問題 1・2問目 sizeA4.pdf (170 ダウンロード)動点問題 3・4問目 sizeA4.pdf (126 ダウンロード)
動点の文章問題を解く時の手順
動点の問題を解くには手順が4つあります。まずはサラッと確認しておいて下さい。具体的には問題を解いていくことで何を意味しているのかわかるようになります。
- 問われているものを文字にする
- 必要な部分の長さを文字式で表す
- 方程式を作る
- 方程式の解が正しいものか確かめる
では模擬授業を始めます。

問題1:動点の移動距離を出す
先生:では授業をはじめます。気をつけ、礼。お願いします!今日は数学の2次方程式応用問題を扱っていくよ。動点の問題だ。
生徒:うわー、あの点が動くやつですか。
先生:そう。中2の1次関数の単現で出てきていて、苦手とする人が多かったね。でも大丈夫。手順どおりに作業をしていけば解けるから。そしてそれを4問解いて慣れればマスターできるよ。まず手順を4つ紹介しよう。
- 問われているものを文字にする
- 必要な部分の長さを文字式で表す
- 方程式を作る
- 方程式の解が正しいものか確かめる
先生:この通りにやっていけば答えを出せるようになるよ。では早速問題を1つ出すから、一緒に解いて行こう。
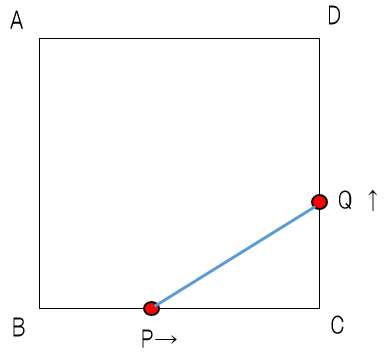
先生:ではまず手順1だ。方程式の文章問題だから文字はxを使っていこう。そして「点PがBから何cm動いたときですか」と聞かれているから、xcm動いたとするよ(=BPの長さ)。このように問われているものを文字にするのが手順1だ。そして手順2に移って…
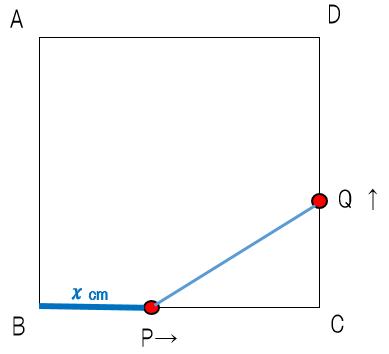
先生:BP=xcm(青い部分)ということだね。このように必要な部分の長さを文字式で表していこう。ちなみに正方形の1辺の長さが6cmだったね。では聞くけどPCの長さは何cmと表せる?
生徒:6-x(cm)
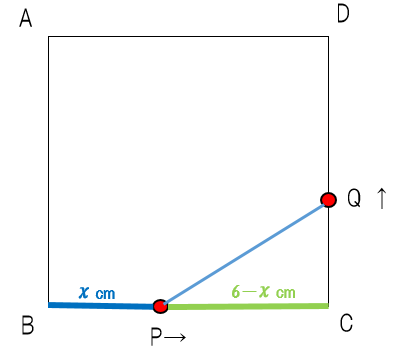
先生:いいね、正解。上の図で言うとBCの長さが6cmだから、そこから余計な長さであるxを引けばPCの長さが出てくるね。だから 6-x(緑の部分)だ。そうしたら次、CQの長さは何cmと表せる?
生徒:x(cm)
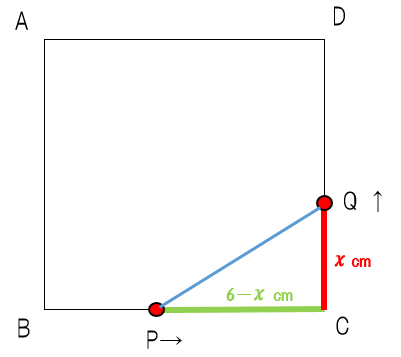
先生:いいね!「点Qは点Pと同時に同じ速さで動き出し」とあるから、BP=CQだね。ということでBPと同じ長さのx(cm)だ。そうしたら必要な部分の長さは文字式で表すことができたので手順3に進もう。問題の文章をもう一度載せておくから読んで方程式を作ってみて。

先生:では方程式言って。
生徒:
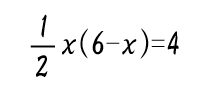
先生:ナイス、正解!「△QPCの面積が4㎠になる」とあるから「△QPC=4」ということだね。三角形の面積を出すには「底辺×高さ÷2」で求められるから底辺のPC=6-xと高さのQC=xを掛けて2で割ろう。2で割るということは「×1/2」でもいいよね。ということで…

先生:このようになる。掛け算を省略して1/2を前に出すなど調節して書くと、言ってくれた通り…
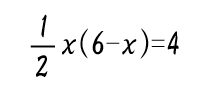
先生:この方程式ができるね。方程式ができたので解いてみて。
・
・
・
先生:解は何になった?
生徒:x=2,4
先生:いいね。途中式を紹介すると以下の通りだ。
まず両辺を2倍して x(6-x)=8
展開して 6x-x2=8(x2はxの2乗です)
左辺で並び換えて -x2+6x-8=0
両辺に-1をかけて x2-6x+8=0
左辺を因数分解して (x-2)(x-4)=0
解は x=2, 4
先生:つまり「点Pが 2cm と 4cm 動いたとき」というのが仮の答えになるね。最後に手順4だ。点Pは2cm進むことはできるのか、4cm進むことは出来るのか確かめよう。両方どう?
生徒:進められる
先生:そうだね。正方形の1辺の長さが6cmだけど、2cm も 4cm も1辺の長さを超えていない。両方とも解として有り得るね。問題の意図に適しているということで、答えは以下の通りだ。
問題2:何秒後なのか時間を出す
先生:では2問目に移ろう。今回は何秒後になるのかを求める問題だけど、さっきと同じ手順でやっていけば答えまでたどり着けるよ。チャレンジしたい人は、自力で解いてみてね。
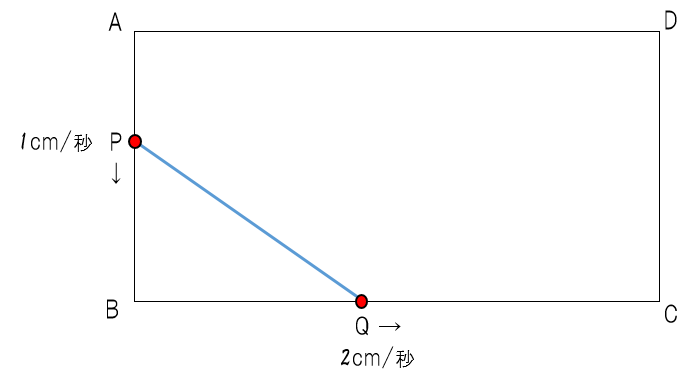
先生:ではやっていこう。まずは手順1ね。「動き出して何秒たったときですか」と聞いているから、「x秒たったとき」としよう。そうすると、今回はx秒後の長さを文字式で表していくのが手順2でやることになるね。では聞くけど、x秒後のAPの長さは?
生徒:x(cm)
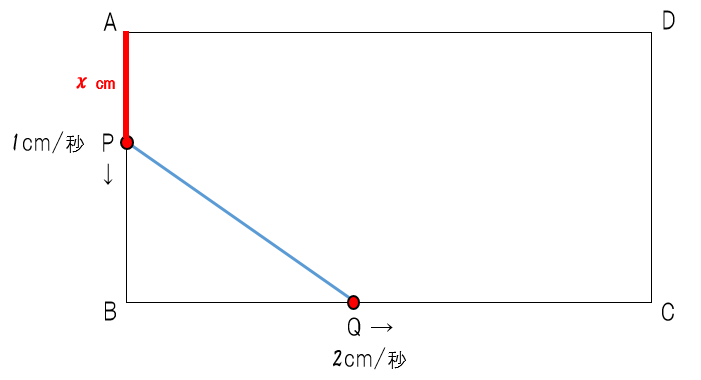
先生:いいね。1秒で1cm進む速さは秒数と進んだ距離が同じ数字になるね。だからx秒後はxcmだ(赤の部分)。そうすると、今回は「△PBQ= 15 」という方程式を作ることになるから、三角形PBQの底辺と高さを文字式で表すことになるね。具体的にはPBとBQが底辺と高さだ。では長方形の縦の長さが8cmとなっていて、PBの長さはどう表せる?
生徒:8-x(cm)
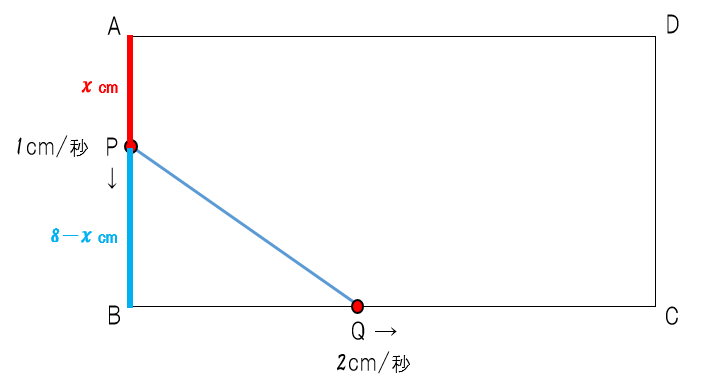
先生:ナイス、正解!ABの長さである8cmから余計な長さであるAPの長さxを引けば良かったね。だから8-xだ(青い部分)。そうするとBQの長さは?
生徒:2x(cm)
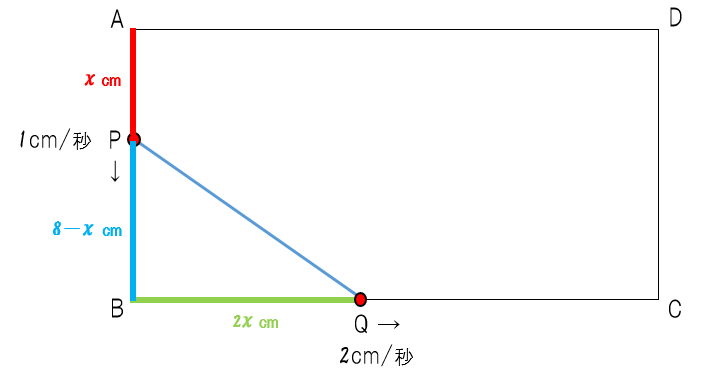
先生:素晴らしい!今回点Qは点Pの2倍の速さで動いているね。だから移動した距離もAPの長さの2倍となって、2xとなるんだ(緑の部分)。ということで、もう気づいたね。三角形の面積が問題で出ているから、その面積を出すために必要な部分を文字式で表せばいいんだ。その後は手順3、方程式を作ろう。作るとどうなる?
・
・
・
生徒:
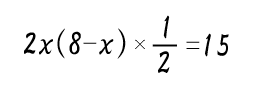
先生:素晴らしいね、正解だ。BC(2x)を三角形の底辺として、それに高さであるPB(8-x)を掛けて最後に1/2を掛けた式にしたね。正解!ではこの方程式を解いて、足しかめをして、答え出してみて。
・
・
・
先生:では聞くけど、答えは何?
生徒:3秒後,5秒後
先生:正解だ、良く出来ました!途中式は以下の通りだよ。
2xの2と1/2の2を約分して x(8-x)=15
展開して 8x-x2=15 (x2はxの2乗です)
左辺で並び換えて -x2+8x-15=0
両辺に-1をかけて x2-8x+15=0
左辺を因数分解して (x-3)(x-5)=0
解は x=3, 5
先生:解が問題の意図に適しているかのチェックだけど、今回も両方とも問題ないね。8秒後には両方の点が動ききってしまうけど、8秒以下に収まっているので適している。だから…
問題3:動点の距離を出す
先生:ここからは自力でやってもらおう。問題3と問題4を解いて下さい。はじめ!(解き終わったらここに戻ってきて解答・解説を確認してくださいね。)
・
・
・
先生:では答えを合わせよう。答えは何になった?
生徒:4cm,6cm
先生:正解、よく出来ました!では以下解説を入れるよ。
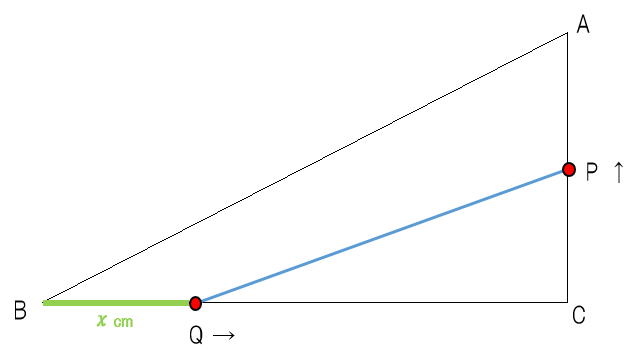
先生:今回は「点QがBから何cm動いたときですか」と聞いているから、BQの長さをxとしよう(緑の部分)。
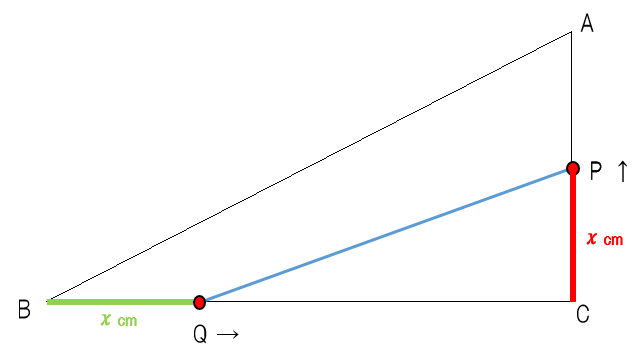
そうすると、点Pと点Qは同じ速さで移動しているので、CPの長さもBQと同じxになるね(赤の部分)。
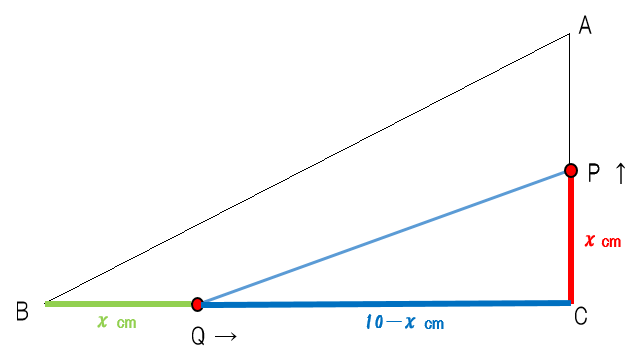
先生:更にBCの長さ10からBQの長さxを引いてQCの長さを10-xと出そう(青い部分)。これで三角形PQCの底辺と高さを文字式で表すことができた。そうしたら底辺×高さ÷2の式に当てはめて2次方程式になおそう。
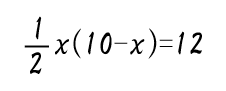
先生:このようになるね。これを解くとx=4,6 と解が出るよ。途中式を紹介すると以下の通りだ。
まず両辺を2倍して x(10-x)=24
展開して 10x-x2=24 (x2はxの2乗です)
左辺で並び換えて -x2+10x-24=0
両辺に-1をかけてx2-10x+24=0
左辺を因数分解して (x-6)(x-4)=0
解は x=4, 6
先生:三角形のACの長さ6cmに注目して、xが6 以下の範囲に収まっていないといけないね。今回はちょうど6cm進みきったところになるけど、有り得る。だから…
問題4:何秒後なのか時間を出す
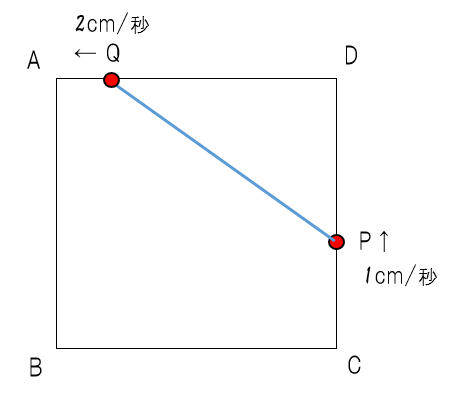
・
・
・
先生:では答え合わせをしよう。何になった?
生徒:3秒後と7秒後
先生:おっしい!答えは「3秒後」なんだ。7秒後は点Qが14cm移動したことになってしまって、1辺の長さ10cmを超えているから有り得ないよ。問題の意図より答えとして不適格なんだ。
先生:では以下解説をしていこう。まず「x秒後」に三角形の面積が21㎠ になるとしよう。そうすると…
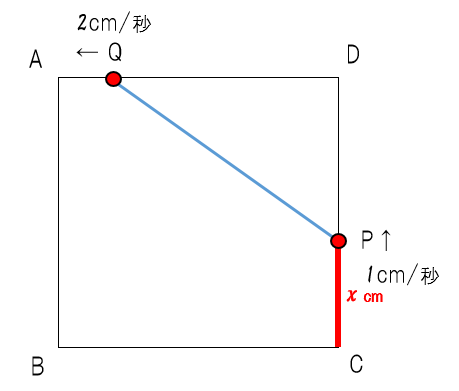
先生:まずCPの長さがxと出るね(赤い部分)。そうすると、その上の部分のPDが…
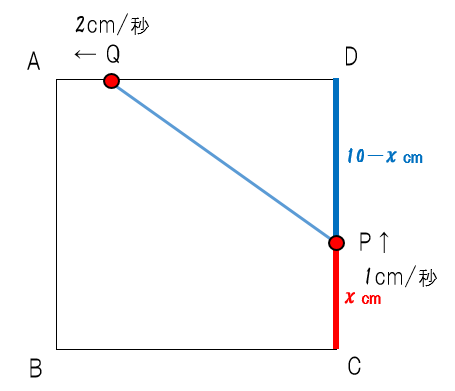
先生:10-xと表せるね(青い部分)。1辺の長さ10cmから余計なPCの長さxcmを引けばいいんだ。さらにQDの長さも出していこう。点Qは点Pより速度が2倍なので…
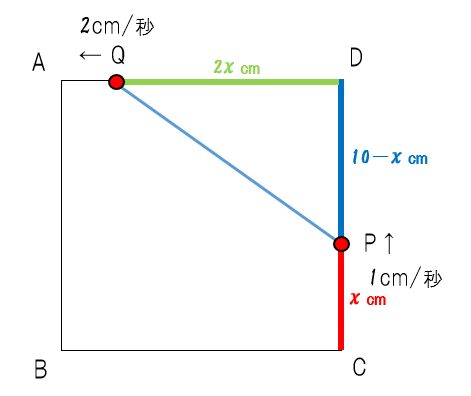
先生:上の図のようにPCの2倍の長さである2xであるとわかるね(緑の部分)。ここまでで三角形の底辺と高さの両方を文字式で表すことが出来た。そこで「△QPD=21」となる方程式を作ろう。そうすると…
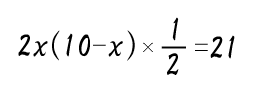
先生:方程式がこのようになるね。途中式を紹介すると以下の通りだ。
2xの2と1/2の2を約分して x(10-x)=21
展開して10x-x2=21
左辺で並び換えて -x2+10x-21=0
両辺に-1をかけて x2-10x+21=0
左辺を因数分解して (x-3)(x-7)=0
解は x=3, 7
先生:解が X=3, 7 と出たので仮の答えが3秒後と7秒後になるね。ただし1辺10cmを秒速2秒で動くと5秒で移動しきってしまうね。つまりxは5以下に収まっていないといけないわけだ。x=7 は問題の意図には不適格ということで…
いかがでしたか。お役に立てれば嬉しいです。最後まで読んでいただいてありがとうございました。ではまた!
中2の「1次関数・動点とグラフ問題」を復習したい方は以下の授業をご覧下さい。